newstarctf-crypto复现

newstarctf
赛题
发布日期:   2025-06-12

week1

Base

题目描述：

1
2
3
This is a base question!

4C4A575851324332474E324547554B494A5A4446513653434E564D444154545A4B354D45454D434E4959345536544B474D5134513D3D3D3D

考点：base 系列编码

赛博厨子一把梭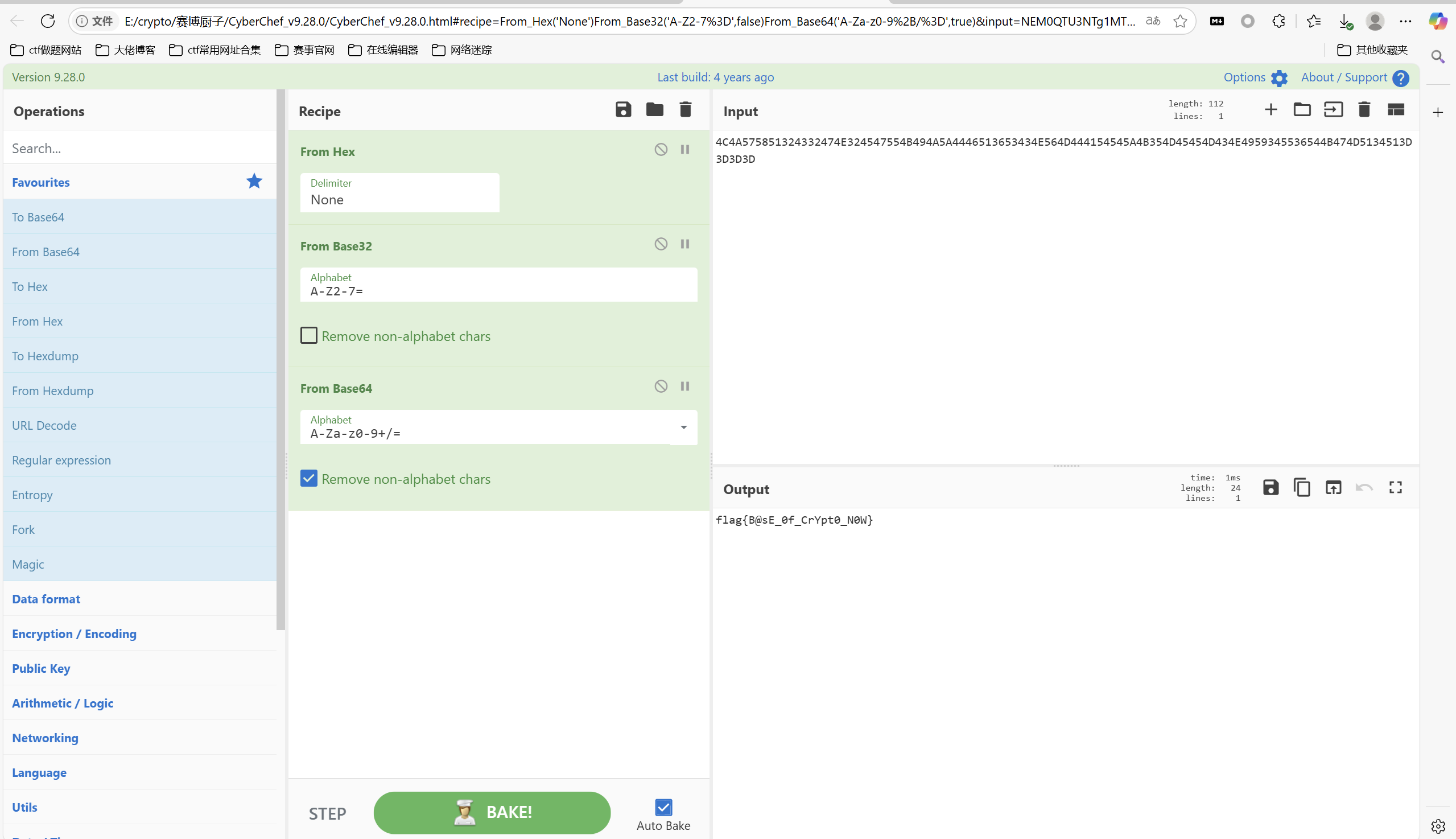

最后flag为

1
flag{B@sE_0f_CrYpt0_N0W}

Strange King

题目描述：

1
某喜欢抽锐刻 5 的皇帝想每天进步一些，直到他娶了个模，回到原点，全部白给😅 这是他最后留下的讯息：ksjr{EcxvpdErSvcDgdgEzxqjql}，flag 包裹的是可读的明文

考点：变异凯撒

题目描述中的皇帝是凯撒皇帝，key是5，凯撒解密发现有一个递增 2 的规律，为了避免超出字母表范围，模的话是对应的 0-25，我们再模一个 26

exp:

1
2
3
4
5
6
7
8
9
10
11
12
txt = 'ksjr{EcxvpdErSvcDgdgEzxqjql}'
plain = ''
i = 5
for j in txt:
    if j.islower():
        plain = plain + chr(97 + (ord(j) - i - 97)%26)
    elif j.isupper():
        plain = plain + chr(65 + (ord(j) - i - 65)%26)
    else:
        plain = plain + j
    i += 2
print(plain)

运行得到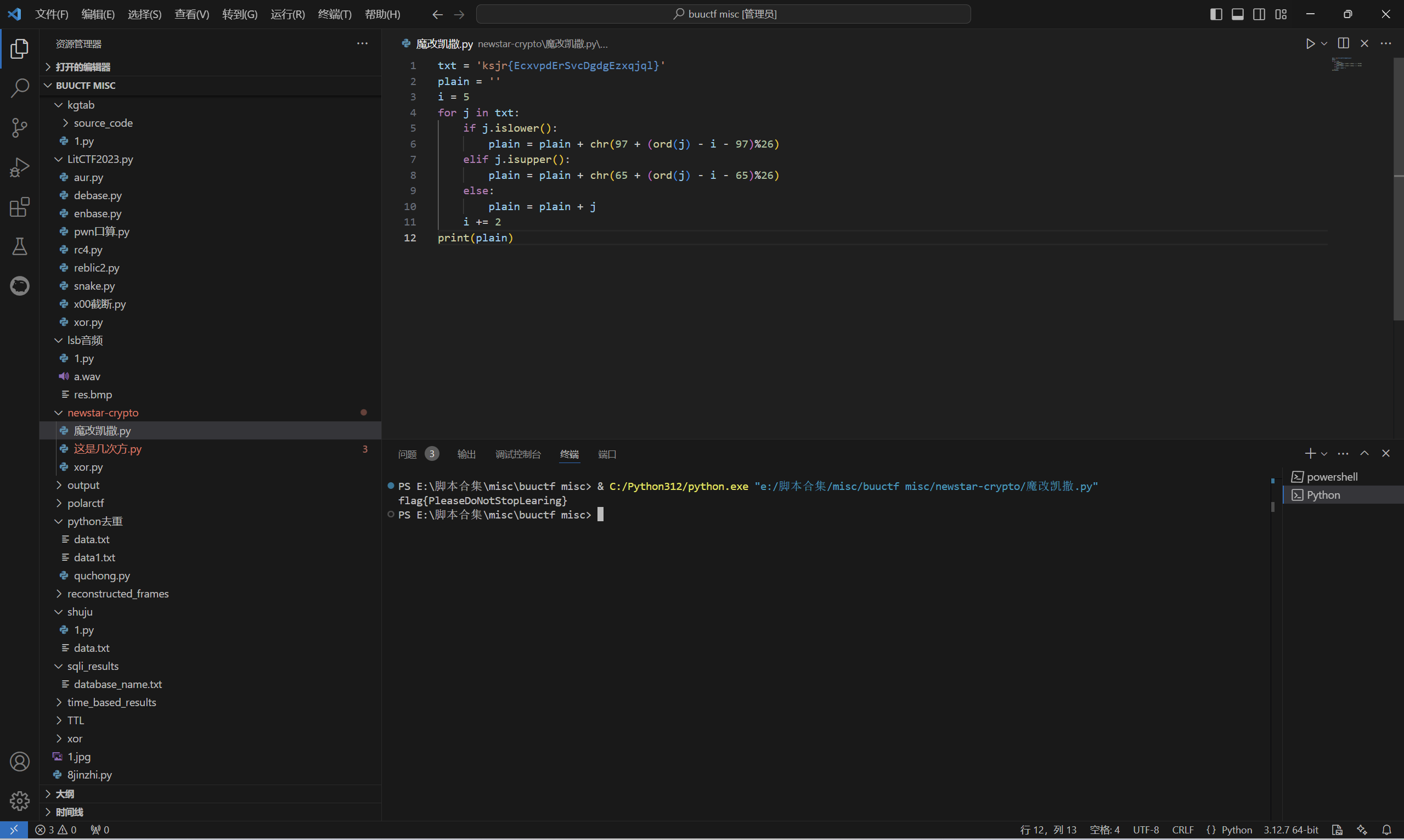

最后flag为

1
flag{PleaseDoNotStopLearing}

xor

题目描述：

1
如果再来一次的话，就能回到从前，一切都会好起来的😭

下载附件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#As a freshman starting in 2024, you should know something about XOR, so this task is for you to sign in.

from pwn import xor
#The Python pwntools library has a convenient xor() function that can XOR together data of different types and lengths
from Crypto.Util.number import bytes_to_long

key = b'New_Star_CTF'
flag='flag{*******************}'

m1 = bytes_to_long(bytes(flag[:13], encoding='utf-8'))
m2 = flag[13:]

c1 = m1 ^ bytes_to_long(key)
c2 = xor(key, m2)
print('c1=',c1)
print('c2=',c2)

'''
c1= 8091799978721254458294926060841
c2= b';:\x1c1<\x03>*\x10\x11u;'
'''

考点:异或

exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
from pwn import xor
from Crypto.Util.number import long_to_bytes, bytes_to_long

# 已知数据
key = b'New_Star_CTF'
c1 = 8091799978721254458294926060841
c2 = b';:\x1c1<\x03>*\x10\x11u;'

# 解密第一部分 (flag的前13个字符)
key_long = bytes_to_long(key)
m1_long = c1 ^ key_long
m1 = long_to_bytes(m1_long).decode('utf-8')

# 解密第二部分 (flag的剩余部分)
m2 = xor(key, c2).decode('utf-8')

# 组合得到完整flag
flag = m1 + m2

print(f"解密后的flag: {flag}")

运行得到

最后flag为

1
flag{0ops!_you_know_XOR!}

一眼秒了

题目描述：

1
n 小小的也很可爱

下载附件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
from Crypto.Util.number import *
from gmpy2 import *
from serct import flag
p = getPrime(512)
q = getPrime(512)
n = p*q
m = bytes_to_long(flag)
e = 65537
c = powmod(m, e, n)
print(n)
print(c)

# 52147017298260357180329101776864095134806848020663558064141648200366079331962132411967917697877875277103045755972006084078559453777291403087575061382674872573336431876500128247133861957730154418461680506403680189755399752882558438393107151815794295272358955300914752523377417192504702798450787430403387076153
# 48757373363225981717076130816529380470563968650367175499612268073517990636849798038662283440350470812898424299904371831068541394247432423751879457624606194334196130444478878533092854342610288522236409554286954091860638388043037601371807379269588474814290382239910358697485110591812060488786552463208464541069

考点:RSA

分解素数n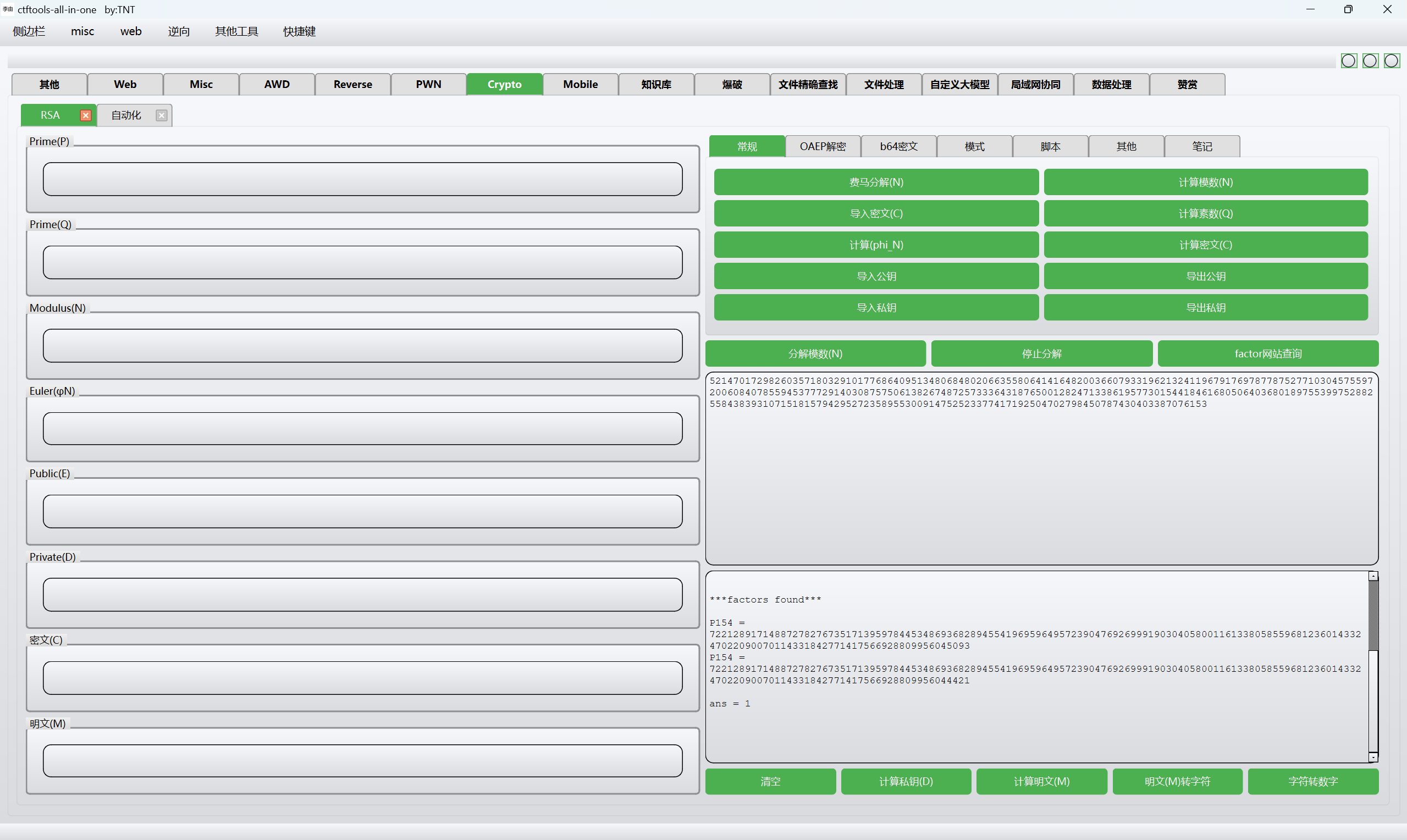

然后一把梭得到flag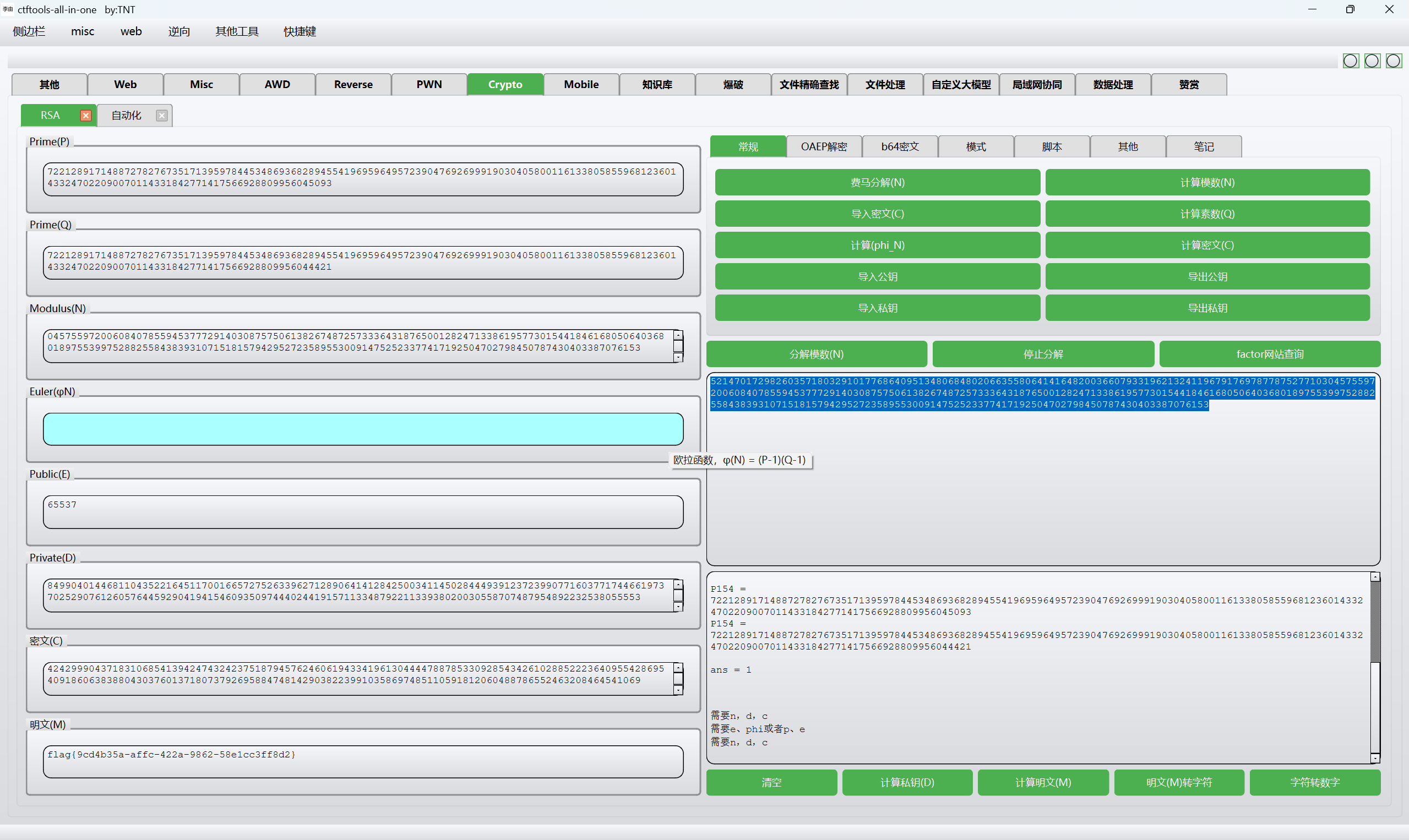

最后flag为

1
flag{9cd4b35a-affc-422a-9862-58e1cc3ff8d2}

week2

Just one and more than two

题目描述：

1
欸，少了少了？😨噢，又多了多了！😱

下载附件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
from Crypto.Util.number import *

flag = b'flag{?????}'
m1 = bytes_to_long(flag[:len(flag)//2])
m2 = bytes_to_long(flag[len(flag)//2:])
e = 65537
p, q, r= (getPrime(512) for _ in range(3))
N=p*q*r
c1 = pow(m1, e, p)
c2 = pow(m2, e, N)

print(f'p={p}\nq={q}\nr={r}\nc1={c1}\nc2={c2}')

'''
p=11867061353246233251584761575576071264056514705066766922825303434965272105673287382545586304271607224747442087588050625742380204503331976589883604074235133
q=11873178589368883675890917699819207736397010385081364225879431054112944129299850257938753554259645705535337054802699202512825107090843889676443867510412393
r=12897499208983423232868869100223973634537663127759671894357936868650239679942565058234189535395732577137079689110541612150759420022709417457551292448732371
c1=8705739659634329013157482960027934795454950884941966136315983526808527784650002967954059125075894300750418062742140200130188545338806355927273170470295451
c2=1004454248332792626131205259568148422136121342421144637194771487691844257449866491626726822289975189661332527496380578001514976911349965774838476334431923162269315555654716024616432373992288127966016197043606785386738961886826177232627159894038652924267065612922880048963182518107479487219900530746076603182269336917003411508524223257315597473638623530380492690984112891827897831400759409394315311767776323920195436460284244090970865474530727893555217020636612445
'''

考点:欧拉函数

解题：

1
2
3
4
5
6
7
8
9
10
11
12
13
第一部分解密：
计算 φ(p) = p-1（因为 p 是素数）
计算 e 在模 φ(p) 下的逆元 d1
使用 d1 解密 c1 得到 m1
将 m1 转换回字节形式
第二部分解密：
计算 φ(N) = (p-1)(q-1)(r-1)
计算 e 在模 φ(N) 下的逆元 d2
使用 d2 解密 c2 得到 m2
将 m2 转换回字节形式
组合结果：
将两部分解密后的字节拼接起来
解码为字符串得到完整 flag

exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
from Crypto.Util.number import *

# 已知参数
p = 11867061353246233251584761575576071264056514705066766922825303434965272105673287382545586304271607224747442087588050625742380204503331976589883604074235133
q = 11873178589368883675890917699819207736397010385081364225879431054112944129299850257938753554259645705535337054802699202512825107090843889676443867510412393
r = 12897499208983423232868869100223973634537663127759671894357936868650239679942565058234189535395732577137079689110541612150759420022709417457551292448732371
c1 = 8705739659634329013157482960027934795454950884941966136315983526808527784650002967954059125075894300750418062742140200130188545338806355927273170470295451
c2 = 1004454248332792626131205259568148422136121342421144637194771487691844257449866491626726822289975189661332527496380578001514976911349965774838476334431923162269315555654716024616432373992288127966016197043606785386738961886826177232627159894038652924267065612922880048963182518107479487219900530746076603182269336917003411508524223257315597473638623530380492690984112891827897831400759409394315311767776323920195436460284244090970865474530727893555217020636612445
e = 65537

# 计算第一部分的解密指数
phi_p = p - 1
d1 = pow(e, -1, phi_p)  # 计算e在模phi_p下的逆元

# 解密第一部分
m1 = pow(c1, d1, p)
m1_bytes = long_to_bytes(m1)

# 计算第二部分的解密指数
phi_N = (p-1) * (q-1) * (r-1)
d2 = pow(e, -1, phi_N)  # 计算e在模phi_N下的逆元

# 解密第二部分
m2 = pow(c2, d2, p*q*r)
m2_bytes = long_to_bytes(m2)

# 组合两部分得到完整flag
flag = m1_bytes + m2_bytes

print(f"解密后的flag: {flag.decode()}")

运行得到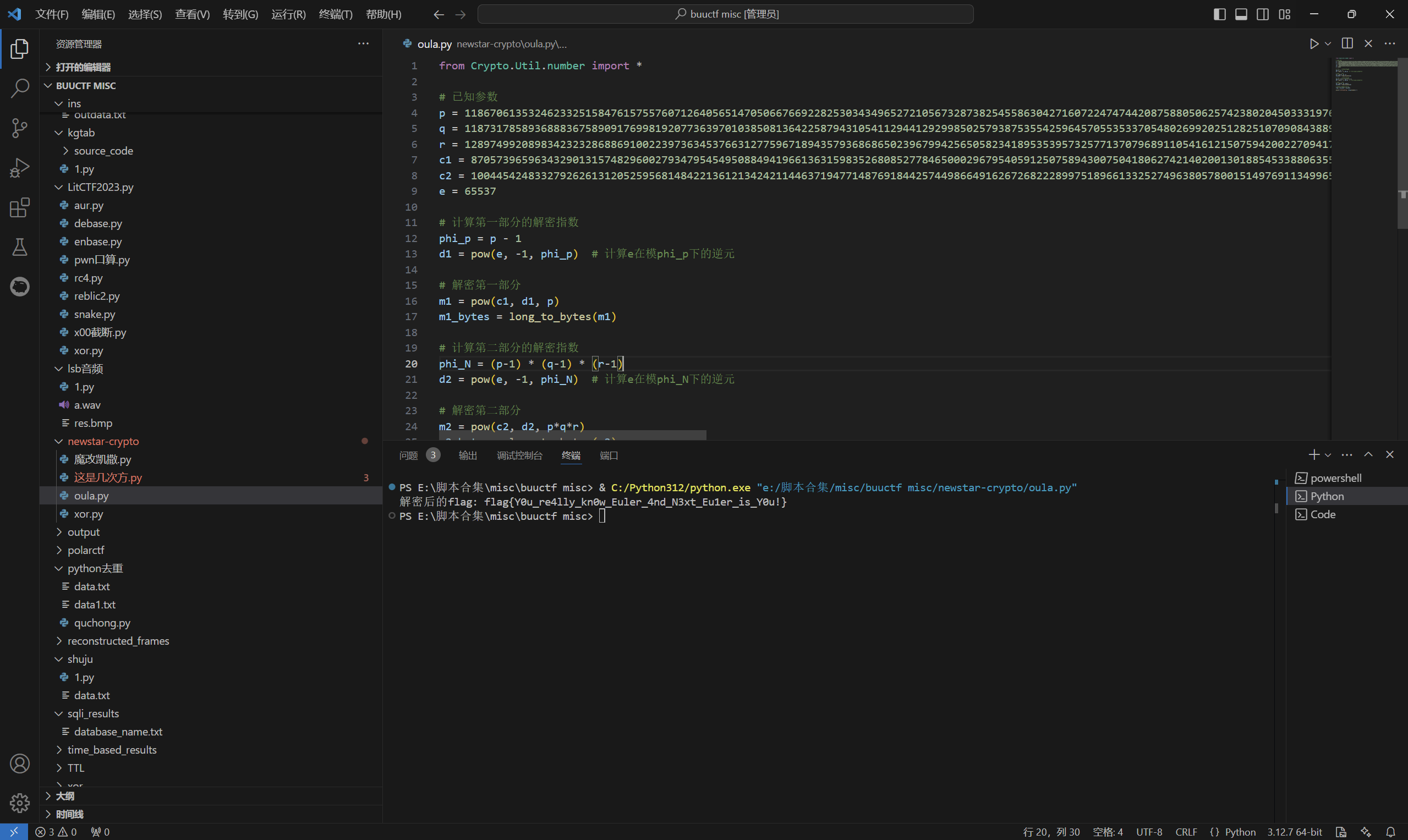

最后flag为

1
flag{Y0u_re4lly_kn0w_Euler_4nd_N3xt_Eu1er_is_Y0u!}

Since you konw something

题目描述：

1
你见到了上周的老朋友，你只需告诉他一部分信息，他就会给你 key

下载附件

1
2
3
4
5
6
7
8
9
10
11
12
13
from pwn import xor
#The Python pwntools library has a convenient xor() function that can XOR together data of different types and lengths
from Crypto.Util.number import bytes_to_long

key = ?? #extremely short
FLAG = 'flag{????????}'
c = bytes_to_long(xor(FLAG,key))

print("c={}".format(c))

'''
c=218950457292639210021937048771508243745941011391746420225459726647571
'''

考点：异或爆破key

exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
from pwn import xor
from Crypto.Util.number import long_to_bytes
from string import ascii_letters

c = 218950457292639210021937048771508243745941011391746420225459726647571
c_bytes = long_to_bytes(c)

# 尝试所有可能的两字符密钥
for i in ascii_letters:
    for j in ascii_letters:
        key = i + j
        decrypted = xor(c_bytes, key)
        
        # 检查解密结果是否包含"flag"
        if b'flag' in decrypted:
            print(f"找到密钥: {key}")
            print(f"解密结果: {decrypted.decode('utf-8', errors='replace')}")

运行得到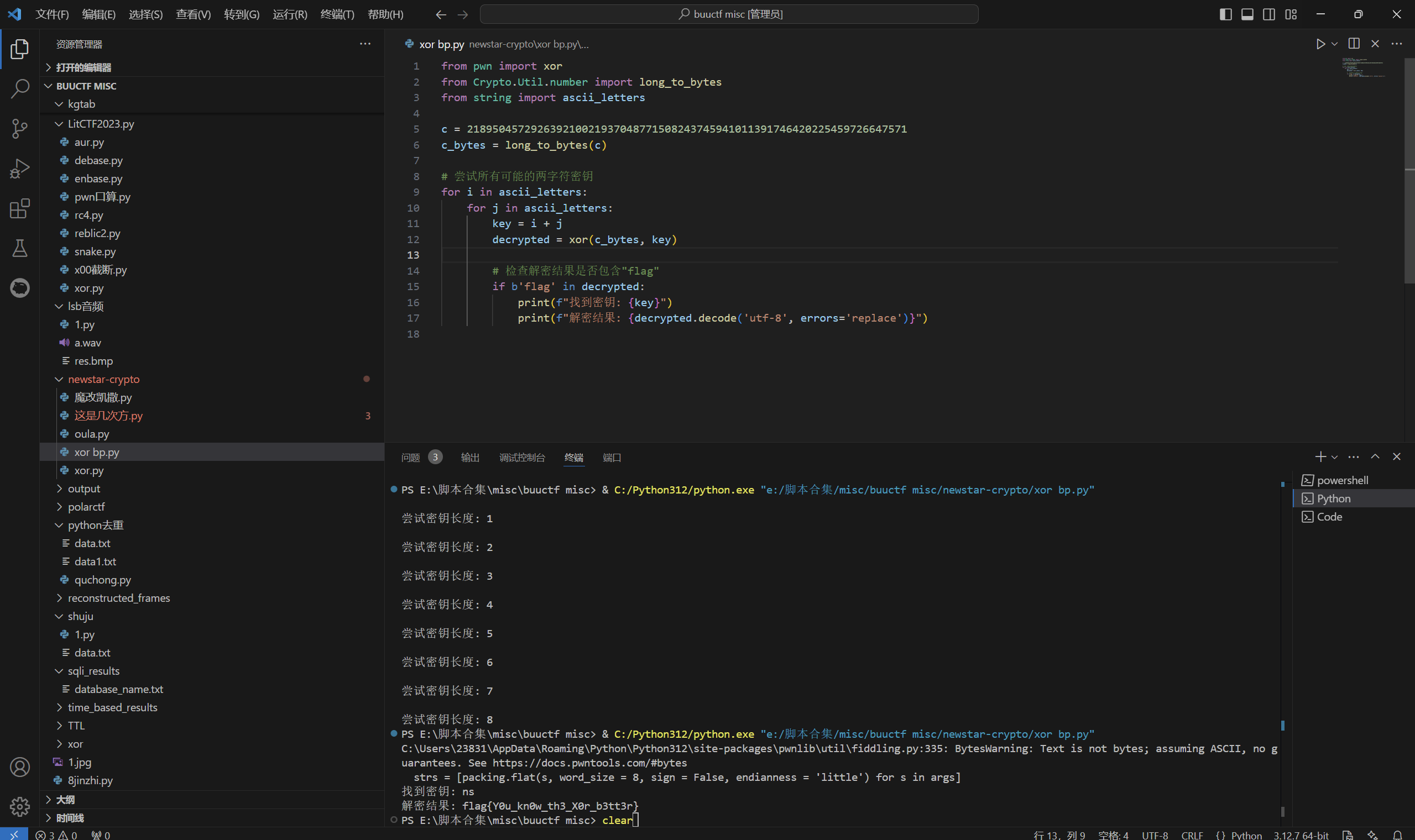

最后flag为

1
flag{Y0u_kn0w_th3_X0r_b3tt3r}

茶里茶气

题目描述：

1
茶？是红茶、绿茶还是奶茶？

下载附件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
from Crypto.Util.number import *

flag = "flag{*****}"
assert len( flag ) == 25

a = ""
for i in flag:
    a += hex(ord(i))[2:]
l = int(a,16).bit_length()
print("l  =" , l )

v0 = int(a,16)>>(l//2)
v1 = int(a,16)-(v0<<(l//2))
p = getPrime(l//2+10)

v2 = 0
derta = 462861781278454071588539315363
v3 = 489552116384728571199414424951
v4 = 469728069391226765421086670817
v5 = 564098252372959621721124077407
v6 = 335640247620454039831329381071
assert v1 < p and v0 < p and derta < p and v3 < p and v4 < p and v5 < p and v6 < p 

for i in range(32):
    v1 += (v0+v2) ^ ( 8*v0 + v3 ) ^ ( (v0>>7) + v4 ) ; v1 %= p
    v0 += (v1+v2) ^ ( 8*v1 + v5 ) ^ ( (v1>>7) + v6 ) ; v0 %= p
    v2 += derta ; v2 %= p

print( "p  =" , p  )
print( "v0 =" , v0 )
print( "v1 =" , v1 )

"""
l  = 199
p  = 446302455051275584229157195942211
v0 = 190997821330413928409069858571234
v1 = 137340509740671759939138452113480
"""

考点:TEA算法

还原算法即可

解题思路

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
代码解析：
初始化变量：

大整数 v0 到 v6、delta、p 等用于加密运算

p = 446302455051275584229157195942211 是模数（229位素数）

第一阶段循环：

python
for i in range(32):
    v2 = (v2 + delta) % p  # 累计增加delta 32次
结果：v2 = (32 × delta) % p

第二阶段循环（核心解密）：

python
for i in range(32):
    v2 = (v2 - delta) % p  # 每次减delta
    # 使用位运算和模运算更新v0和v1
    v0 = (v0 - ((v1+v2) ^ (8*v1+v5) ^ ((v1>>7)+v6))) % p
    v1 = (v1 - ((v0+v2) ^ (8*v0+v3) ^ ((v0>>7)+v4))) % p
每轮迭代中：

v2 递减：从 32×delta → 31×delta → ... → 0

v0 和 v1 通过位运算（异或、移位）相互更新

结果组合：

python
a = hex((v0 << (l//2)) + v1)[2:]  # l=199, 左移99位后拼接v1
将 v0 左移99位后加上 v1

转换为十六进制字符串（去掉前缀 0x）

HEX转ASCII

exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
v2 = 0
delta = 462861781278454071588539315363
v3 = 489552116384728571199414424951
v4 = 469728069391226765421086670817
v5 = 564098252372959621721124077407
v6 = 335640247620454039831329381071
l  = 199
p  = 446302455051275584229157195942211
v0 = 190997821330413928409069858571234
v1 = 137340509740671759939138452113480

for i in range( 32 ):
    v2 += delta ; v2 %= p

for i in range(32):
    v2 -= delta ; v2 %= p
    v0 -= (v1+v2) ^ ( 8*v1 + v5 ) ^ ( (v1>>7) + v6 ) ; v0 %= p
    v1 -= (v0+v2) ^ ( 8*v0 + v3 ) ^ ( (v0>>7) + v4 ) ; v1 %= p

a = hex((v0<<((l//2))) + v1)[2:]
print(a)
flag = ""
for i in range(0,len(a),2):
    flag+=chr(int(a[i]+a[i+1],16))
print(flag)

运行得到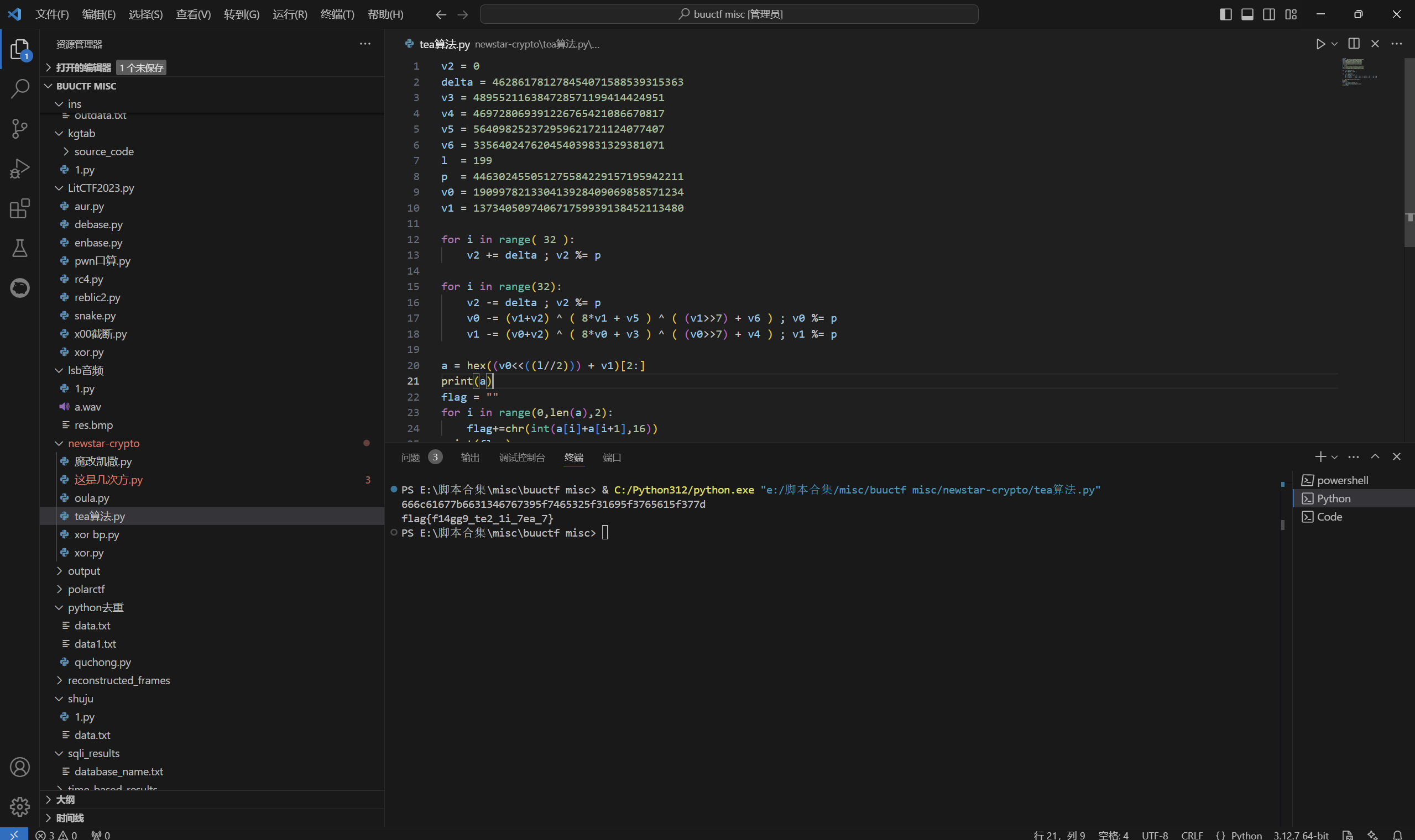

最后flag为

1
flag{f14gg9_te2_1i_7ea_7}

这是几次方？疑惑！

题目描述：

1
2
3
^ w ^

^ 在 python 里面到底是什么意思？不如先看看大 python 运算符号的优先级吧

下载附件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
from Crypto.Util.number import *


flag = b'flag{*****}'
p = getPrime(512)
q = getPrime(512)
n = p*q
e = 65537

m = bytes_to_long(flag)
c = pow(m, e, n)

hint = p^e + 10086

print("c =", c)
print("[n, e] =", [n, e])
print("hint =", hint)
'''
c = 36513006092776816463005807690891878445084897511693065366878424579653926750135820835708001956534802873403195178517427725389634058598049226914694122804888321427912070308432512908833529417531492965615348806470164107231108504308584954154513331333004804817854315094324454847081460199485733298227480134551273155762
[n, e] = [124455847177872829086850368685666872009698526875425204001499218854100257535484730033567552600005229013042351828575037023159889870271253559515001300645102569745482135768148755333759957370341658601268473878114399708702841974488367343570414404038862892863275173656133199924484523427712604601606674219929087411261, 65537]
hint = 12578819356802034679792891975754306960297043516674290901441811200649679289740456805726985390445432800908006773857670255951581884098015799603908242531673390
'''

考点:异或符号的运算优先级

在 Python 中异或先计算两边，再进行异或操作

所有 hint 是 p 和 e+10086 的异或结果,可以求p

1
p=hint^(e+10086)

exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
from Crypto.Util.number import *

# 已知参数
c = 36513006092776816463005807690891878445084897511693065366878424579653926750135820835708001956534802873403195178517427725389634058598049226914694122804888321427912070308432512908833529417531492965615348806470164107231108504308584954154513331333004804817854315094324454847081460199485733298227480134551273155762
n = 124455847177872829086850368685666872009698526875425204001499218854100257535484730033567552600005229013042351828575037023159889870271253559515001300645102569745482135768148755333759957370341658601268473878114399708702841974488367343570414404038862892863275173656133199924484523427712604601606674219929087411261
e = 65537
hint = 12578819356802034679792891975754306960297043516674290901441811200649679289740456805726985390445432800908006773857670255951581884098015799603908242531673390

# 从hint中恢复p
p=hint^(e+10086)



q = n // p

phi = (p - 1) * (q - 1)
d = inverse(e, phi)
m = pow(c, d, n)
print(long_to_bytes(m))

运行得到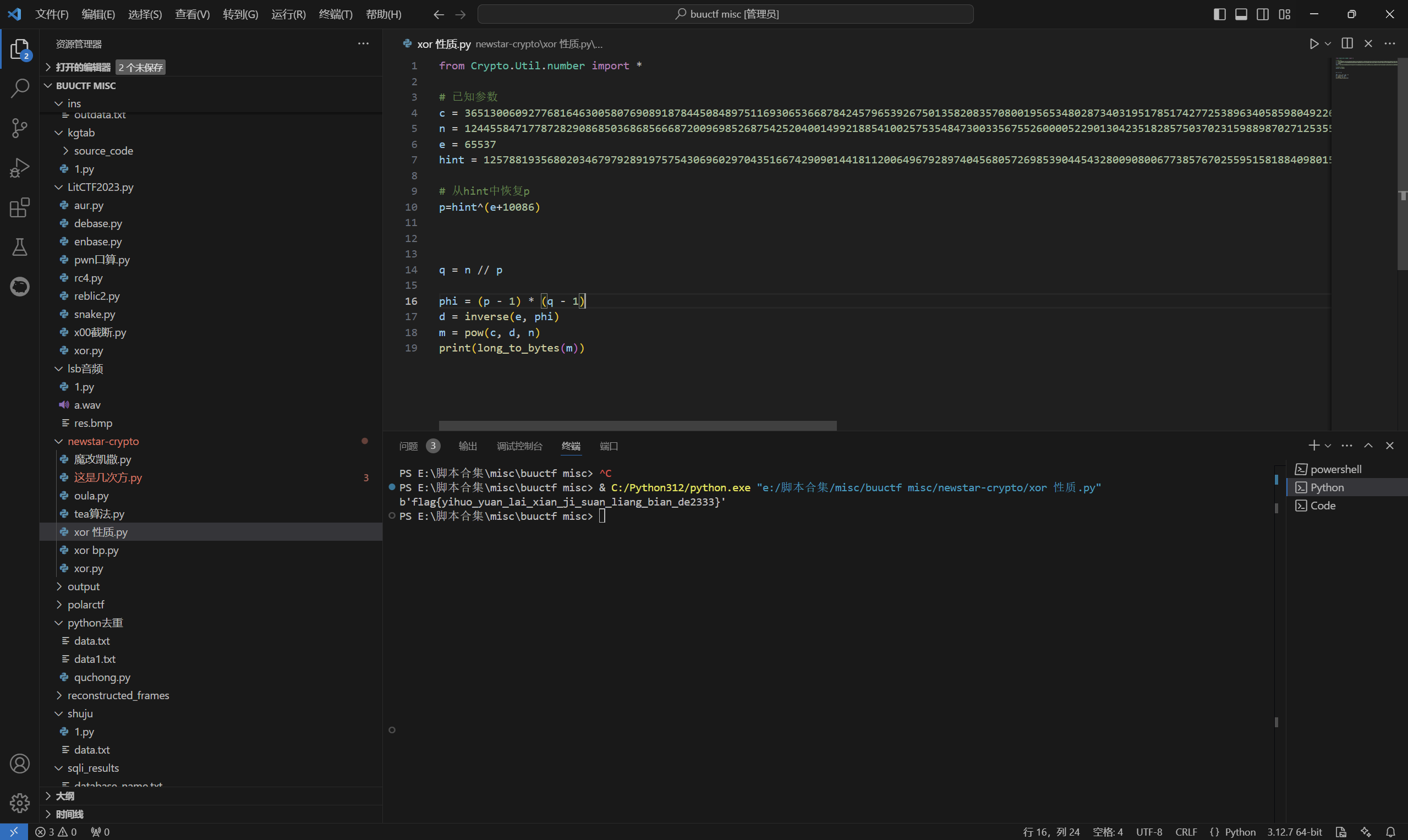

最后flag为

1
flag{yihuo_yuan_lai_xian_ji_suan_liang_bian_de2333}

week3

不用谢喵

题目描述：

1
2
3
——求求你帮我解密吧，我什么都会做的😭

——解好了，不用谢喵😸。（都解好密了所以是签到捏）

下载附件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
from Crypto.Cipher import AES
from Crypto.Util.number import *
import os

KEY = b"fake_key_fake_ke"
FLAG = "flag{fake_flag_fake_flag}"  

def decrypt(c):
    AES_ECB = AES.new(KEY, AES.MODE_ECB)
    decrypted = AES_ECB.decrypt(long_to_bytes(c))

    return decrypted.hex()

def encrypt():
    iv = os.urandom(16)
    AES_CBC = AES.new(KEY, AES.MODE_CBC, iv)
    encrypted = AES_CBC.encrypt(FLAG.encode())
    print('iv:',iv.hex())

    return iv.hex() + encrypted.hex()

c=encrypt()
print('encrypt:',c)
print('decrypt:',decrypt(int(c,16)))

#encrypt: f2040fe3063a5b6c65f66e1d2bf47b4cddb206e4ddcf7524932d25e92d57d3468398730b59df851cbac6d65073f9e138
#什么是AES啊😭，求求你帮我解密吧，我什么都会做的！！！！！😭

'''
什么都会做？那就去学习一下AES的工作模式吧……
我这次就先给你解一下好了，不用谢喵
decrypt: f9899749fec184d81afecd35da430bc394686e847d72141b3a955a4f6e920e7d91cb599d92ba2a6ba51860bb5b32f23b
这对吗？哦不对不对，哦对的对的。
'''

考点:AES算法

解题思路

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
AES-CBC模式加密过程：

第一块明文：m0 = AES_encrypt(IV ⊕ plaintext_block1)

第二块明文：m1 = AES_encrypt(c0 ⊕ plaintext_block2)

利用ECB解密输出：

解密函数输出包含：

d1 = AES_decrypt(c0)

d2 = AES_decrypt(c1)

通过CBC解密公式：

plaintext_block1 = IV ⊕ d1

plaintext_block2 = c0 ⊕ d2

虽然不知道KEY，但利用解密函数的输出间接获得了AES解密结果
通过异或操作还原原始明文

exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
from Crypto.Cipher import AES

# 给定的加密输出
encrypt_str = "f2040fe3063a5b6c65f66e1d2bf47b4cddb206e4ddcf7524932d25e92d57d3468398730b59df851cbac6d65073f9e138"

# 从解密函数得到的输出（包含关键信息）
decrypt_output = "f9899749fec184d81afecd35da430bc394686e847d72141b3a955a4f6e920e7d91cb599d92ba2a6ba51860bb5b32f23b"

# 分解加密字符串：前32字符=IV(16字节)，剩余64字符=密文(32字节)
iv_hex = encrypt_str[:32]
ciphertext_hex = encrypt_str[32:]

# 分解解密输出：3个16字节块
d0 = bytes.fromhex(decrypt_output[:32])  # 对应IV的解密
d1 = bytes.fromhex(decrypt_output[32:64])  # 对应第一个密文块的解密
d2 = bytes.fromhex(decrypt_output[64:])  # 对应第二个密文块的解密

# 提取原始字节
iv = bytes.fromhex(iv_hex)
c0 = bytes.fromhex(ciphertext_hex[:32])  # 第一个密文块
c1 = bytes.fromhex(ciphertext_hex[32:])  # 第二个密文块

# CBC模式解密原理：
# 明文块1 = AES解密(密文块1) XOR IV
# 明文块2 = AES解密(密文块2) XOR 密文块1

# 使用解密输出中的d1作为AES解密(c0)的结果
plaintext_block1 = bytes([d1[i] ^ iv[i] for i in range(16)])

# 使用解密输出中的d2作为AES解密(c1)的结果
plaintext_block2 = bytes([d2[i] ^ c0[i] for i in range(16)])

# 组合明文块
flag = plaintext_block1 + plaintext_block2

# 输出结果
print("解密后的FLAG:", flag.decode())

运行得到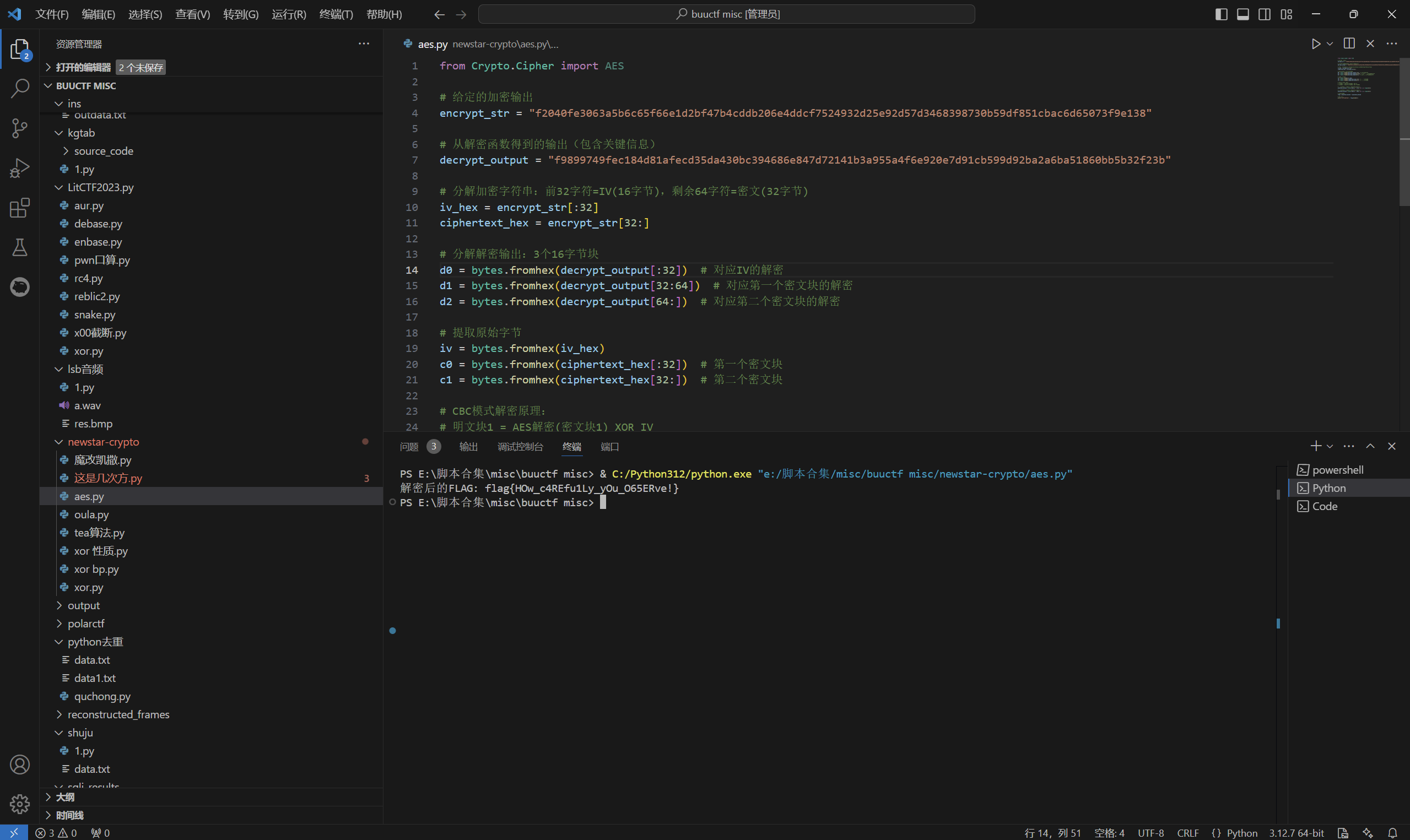

最后flag为

1
flag{HOw_c4REfu1Ly_yOu_O65ERve!}

两个黄鹂鸣翠柳

题目描述：

1
数行白鹭上青天

下载附件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
import random
from Crypto.Util.number import *
while 1:
    delta = getPrime(1024)
    p = getPrime(512)
    q = getPrime(512)
    N = p * q
    if delta<N:
        break
flag = b'flag{xxxxxxxxxxxxx}'
e = getPrime(10)
m = bytes_to_long(flag)
t1 = random.randint(0,255)
t2 = random.randint(0,255)
assert (t1 != t2)
m1 = m + t1 * delta
m2 = m + t2 * delta
c1 = pow(m1, e, N)
c2 = pow(m2, e, N)
print("e = ", e)
print("c1 = ", c1)
print("c2 = ", c2)
print("N = ", N)
print("delta = ", delta)

'''
e =  683
c1 =  56853945083742777151835031127085909289912817644412648006229138906930565421892378967519263900695394136817683446007470305162870097813202468748688129362479266925957012681301414819970269973650684451738803658589294058625694805490606063729675884839653992735321514315629212636876171499519363523608999887425726764249
c2 =  89525609620932397106566856236086132400485172135214174799072934348236088959961943962724231813882442035846313820099772671290019212756417758068415966039157070499263567121772463544541730483766001321510822285099385342314147217002453558227066228845624286511538065701168003387942898754314450759220468473833228762416
N =  147146340154745985154200417058618375509429599847435251644724920667387711123859666574574555771448231548273485628643446732044692508506300681049465249342648733075298434604272203349484744618070620447136333438842371753842299030085718481197229655334445095544366125552367692411589662686093931538970765914004878579967
delta =  93400488537789082145777768934799642730988732687780405889371778084733689728835104694467426911976028935748405411688535952655119354582508139665395171450775071909328192306339433470956958987928467659858731316115874663323404280639312245482055741486933758398266423824044429533774224701791874211606968507262504865993
'''

考点:关联信息攻击，多项式 gcd

参考

Coppersmith 相关攻击 - CTF Wiki

exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
from Crypto.Util.number import *
import binascii
 
def attack(c1, c2, b, e, n):
	PR.<x>=PolynomialRing(Zmod(n))
	g1 = x^e - c1
	g2 = (x+b)^e - c2
 
	def gcd(g1, g2):
		while g2:
			g1, g2 = g2, g1 % g2
		return g1.monic()
	return -gcd(g1, g2)[0]
 
e =  683
c1 =  56853945083742777151835031127085909289912817644412648006229138906930565421892378967519263900695394136817683446007470305162870097813202468748688129362479266925957012681301414819970269973650684451738803658589294058625694805490606063729675884839653992735321514315629212636876171499519363523608999887425726764249
c2 =  89525609620932397106566856236086132400485172135214174799072934348236088959961943962724231813882442035846313820099772671290019212756417758068415966039157070499263567121772463544541730483766001321510822285099385342314147217002453558227066228845624286511538065701168003387942898754314450759220468473833228762416
N =  147146340154745985154200417058618375509429599847435251644724920667387711123859666574574555771448231548273485628643446732044692508506300681049465249342648733075298434604272203349484744618070620447136333438842371753842299030085718481197229655334445095544366125552367692411589662686093931538970765914004878579967
delta =  93400488537789082145777768934799642730988732687780405889371778084733689728835104694467426911976028935748405411688535952655119354582508139665395171450775071909328192306339433470956958987928467659858731316115874663323404280639312245482055741486933758398266423824044429533774224701791874211606968507262504865993
for i in range(256):
	b=-delta*i
	m1=attack(c1,c2,b,e,N)
	print(i)
	for j in range(256):
		flag=(m1-j*delta)%N
		flag=long_to_bytes(int(flag))
		if b'flag' in flag:
			print(flag)
			exit()

运行得到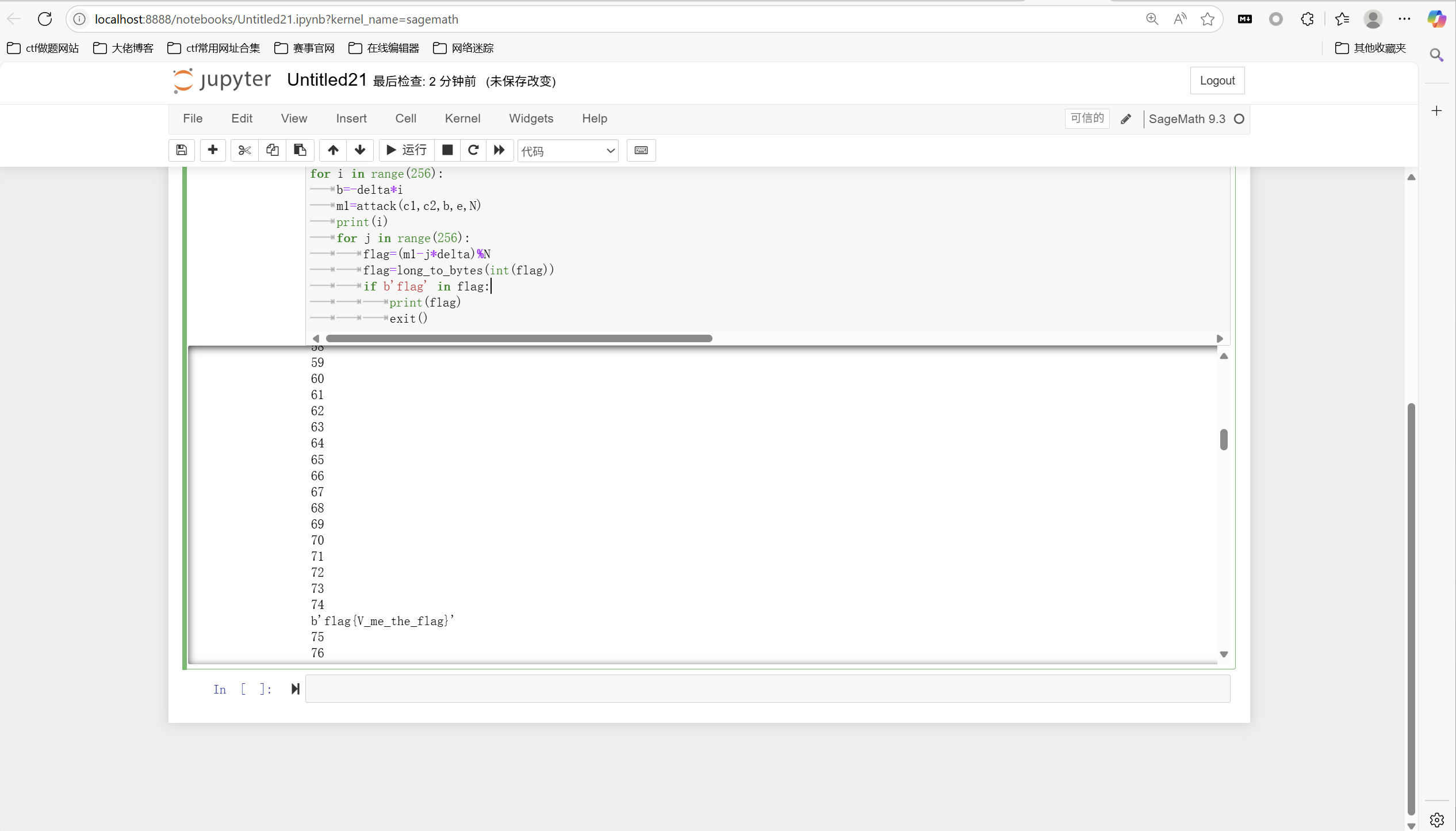

官方做法是

Half-GCD 算法

exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
from Crypto.Util.number import *

def HGCD(a, b):
    if 2 * b.degree() <= a.degree() or a.degree() == 1:
        return 1, 0, 0, 1
    m = a.degree() // 2
    a_top, a_bot = a.quo_rem(x ^ m)
    b_top, b_bot = b.quo_rem(x ^ m)
    R00, R01, R10, R11 = HGCD(a_top, b_top)
    c = R00 * a + R01 * b
    d = R10 * a + R11 * b
    q, e = c.quo_rem(d)
    d_top, d_bot = d.quo_rem(x ^ (m // 2))
    e_top, e_bot = e.quo_rem(x ^ (m // 2))
    S00, S01, S10, S11 = HGCD(d_top, e_top)
    RET00 = S01 * R00 + (S00 - q * S01) * R10
    RET01 = S01 * R01 + (S00 - q * S01) * R11
    RET10 = S11 * R00 + (S10 - q * S11) * R10
    RET11 = S11 * R01 + (S10 - q * S11) * R11
    return RET00, RET01, RET10, RET11

def related_message_attack(a, b):
    q, r = a.quo_rem(b)
    if r == 0:
        return b
    R00, R01, R10, R11 = HGCD(a, b)
    c = R00 * a + R01 * b
    d = R10 * a + R11 * b
    if d == 0:
        return c.monic()
    q, r = c.quo_rem(d)
    if r == 0:
        return d
    return related_message_attack(d, r)

e =  683
c1 =  56853945083742777151835031127085909289912817644412648006229138906930565421892378967519263900695394136817683446007470305162870097813202468748688129362479266925957012681301414819970269973650684451738803658589294058625694805490606063729675884839653992735321514315629212636876171499519363523608999887425726764249
c2 =  89525609620932397106566856236086132400485172135214174799072934348236088959961943962724231813882442035846313820099772671290019212756417758068415966039157070499263567121772463544541730483766001321510822285099385342314147217002453558227066228845624286511538065701168003387942898754314450759220468473833228762416
N =  147146340154745985154200417058618375509429599847435251644724920667387711123859666574574555771448231548273485628643446732044692508506300681049465249342648733075298434604272203349484744618070620447136333438842371753842299030085718481197229655334445095544366125552367692411589662686093931538970765914004878579967
delta =  93400488537789082145777768934799642730988732687780405889371778084733689728835104694467426911976028935748405411688535952655119354582508139665395171450775071909328192306339433470956958987928467659858731316115874663323404280639312245482055741486933758398266423824044429533774224701791874211606968507262504865993

is_flag = False

for delt in range(-255, 255, 8):

    PR.<x> = PolynomialRing(Zmod(N))
    f = x ^ e - c1
    g1 = ((x + (delt + 0) * delta) ^ e - c2) * ((x + (delt + 1) * delta) ^ e - c2)
    g2 = ((x + (delt + 2) * delta) ^ e - c2) * ((x + (delt + 3) * delta) ^ e - c2)
    g3 = ((x + (delt + 4) * delta) ^ e - c2) * ((x + (delt + 5) * delta) ^ e - c2)
    g4 = ((x + (delt + 6) * delta) ^ e - c2) * ((x + (delt + 7) * delta) ^ e - c2)
    if delt == -7:
        g4 = ((x + (delt + 6) * delta) ^ e - c2)
    g = g1 * g2 * g3 * g4
    res = related_message_attack(f, g)
    m1 = int(-res.monic().coefficients()[0])
    for t1 in range(256):
        m = (m1 % N - t1 * delta) % N
        if m > 0:
            flag = long_to_bytes(m)
            if flag[:4] ==b'flag':
                print(flag)
                is_flag = True
                break

    if is_flag:
        break

运行得到

最后flag为

1
flag{V_me_the_flag}

故事新编 1

题目描述：

1
我亦曾无敌人间三百年

下载附件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
from hashlib import md5
zen1  = '''

'''
key1 = 
def enc1(plaintext, key):
    def shift_char(c, k):
        return chr(((ord(c) - ord('A') + (ord(k) - ord('A'))) % 26) + ord('A'))

    plaintext = plaintext.upper()
    key = key.upper()
    ciphertext = []
    key_index = 0

    for char in plaintext:
        if char.isalpha():
            ciphertext.append(shift_char(char, key[key_index % len(key)]))
            key_index += 1
        else:
            ciphertext.append(char)

    return ''.join(ciphertext)
print('enc = \'\'\'' + enc1(zen1, key1)+'\'\'\'')
flag = b'flag{'+md5(zen1.encode()).hexdigest().encode()+b'}'
print(flag)
#----------------------------------------------
enc = '''
TYBNBBZNT WF TYUMMK NAIB HYFZ.
XFIFBKWG AM CXBMYK BVNF CNITBWBB.
GVEJMX QL VXBHRJ NITV VIFXZRP.
WPFXEYQ QG OWNUXZ MBTV QBEJMBKTNXL.
TYSN JL JXNMMF GZUO GMLNXL.
GCSLTX QL VXBHRJ NITV WYGAS.
SDUHT QL PXOSAWLF
KMTXTJWYANZ VWNHMA.
GCWWJTT VULMG NJYO'M AIYVQOY WHPNOA NH JFRSE UAM KOEMG.
NDNIHCZB IZOPLCDTTBNR JSNLM QNZBNR.
MFEGLT LPHOEL BRNYS IILM LQZRFNMR.
CGFXAG RPJMBKBNEG GVDYOVMW.
'''

考点：维吉尼亚爆破

在线网站爆破

Vigenere Solver | guballa.de

然后直接将zen1和key内容填上，运行脚本即可

exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
from hashlib import md5
zen1  = '''
BEAUTIFUL IS BETTER THAN UGLY.
EXPLICIT IS BETTER THAN IMPLICIT.
SIMPLE IS BETTER THAN COMPLEX.
COMPLEX IS BETTER THAN COMPLICATED.
FLAT IS BETTER THAN NESTED.
SPARSE IS BETTER THAN DENSE.
FLAGA IS VEGENERE
READABILITY COUNTS.
SPECIAL CASES AREN'T SPECIAL ENOUGH TO BREAK THE RULES.
ALTHOUGH PRACTICALITY BEATS PURITY.
ERRORS SHOULD NEVER PASS SILENTLY.
UNLESS EXPLICITLY SILENCED.
'''
key1 = "subtitution"
def enc1(plaintext, key):
    def shift_char(c, k):
        return chr(((ord(c) - ord('A') + (ord(k) - ord('A'))) % 26) + ord('A'))

    plaintext = plaintext.upper()
    key = key.upper()
    ciphertext = []
    key_index = 0

    for char in plaintext:
        if char.isalpha():
            ciphertext.append(shift_char(char, key[key_index % len(key)]))
            key_index += 1
        else:
            ciphertext.append(char)

    return ''.join(ciphertext)
print('enc = \'\'\'' + enc1(zen1, key1)+'\'\'\'')
flag = b'flag{'+md5(zen1.encode()).hexdigest().encode()+b'}'
print(flag)
#----------------------------------------------
enc = '''
TYBNBBZNT WF TYUMMK NAIB HYFZ.
XFIFBKWG AM CXBMYK BVNF CNITBWBB.
GVEJMX QL VXBHRJ NITV VIFXZRP.
WPFXEYQ QG OWNUXZ MBTV QBEJMBKTNXL.
TYSN JL JXNMMF GZUO GMLNXL.
GCSLTX QL VXBHRJ NITV WYGAS.
SDUHT QL PXOSAWLF
KMTXTJWYANZ VWNHMA.
GCWWJTT VULMG NJYO'M AIYVQOY WHPNOA NH JFRSE UAM KOEMG.
NDNIHCZB IZOPLCDTTBNR JSNLM QNZBNR.
MFEGLT LPHOEL BRNYS IILM LQZRFNMR.
CGFXAG RPJMBKBNEG GVDYOVMW.
'''

运行得到

最后flag为

1
flag{b14375358eabfea4e405bd2186936289}

故事新编 2

题目描述：

1
生于余烬，归于虚无。

hint：

1
2
请注意首尾的换行符
zen 内全部为大写字符

下载附件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
from hashlib import md5
zen2 = '''

'''
key2 = 
dict1 = {'A': 0, 'B': 1, 'C': 2, 'D': 3, 'E': 4,
         'F': 5, 'G': 6, 'H': 7, 'I': 8, 'J': 9,
         'K': 10, 'L': 11, 'M': 12, 'N': 13, 'O': 14,
         'P': 15, 'Q': 16, 'R': 17, 'S': 18, 'T': 19,
         'U': 20, 'V': 21, 'W': 22, 'X': 23, 'Y': 24, 'Z': 25}

dict2 = {0: 'A', 1: 'B', 2: 'C', 3: 'D', 4: 'E',
         5: 'F', 6: 'G', 7: 'H', 8: 'I', 9: 'J',
         10: 'K', 11: 'L', 12: 'M', 13: 'N', 14: 'O',
         15: 'P', 16: 'Q', 17: 'R', 18: 'S', 19: 'T',
         20: 'U', 21: 'V', 22: 'W', 23: 'X', 24: 'Y', 25: 'Z'}

def generate_key(message, key):
    for i in range(len(message)):
        if message[i].isalpha() == False:
            pass
        else:
            key += message[i]
    return key
def enc2(message, key):
    message = message.upper()
    key = key.upper()
    key_new = generate_key(message, key)
    cipher_text = ''
    i = 0
    for letter in message:
        if letter.isalpha():
            x = (dict1[letter]+dict1[key_new[i]]) % 26
            i += 1
            cipher_text += dict2[x]
        else:
            cipher_text += letter
    return cipher_text
print('enc = \'\'\'' + enc2(zen2, key2)+'\'\'\'')
flag = b'flag{'+md5(zen2.encode()).hexdigest().encode()+b'}'
print(flag)
#----------------------------------------------
enc = '''
AH ILV XUDX WY UFJWTCVMF, VJFWWS YHQ UMSJBTRZSS NG KNLWL.
XTTKE LPCHER HY SFW-- TUH GVWMSLLEMC CAPY BQT --FFAMFUT HYM GZ BC VX.
OMOPCOYD TFTH ZOG FAJ GVH VK VUCIHQS YF FGEGM VRZFNA MIM'RX ICKUA.
HBH MK TCHNVV WBTP URJAZ.
SMXAHYXA UEIRV DW FFEXU PYZARV OLRV JWLAX APA.
BY XYX PMCCMSLGGOPQTG PW PMGO XA IKILTQB, VB'K H BRG BRIX.
XQ TPR QFHLFMHVWETQTG PW MMHJ XA IKILTQB, VB EEY TC T USLS TDMN.
'''

考点：变异维吉尼亚爆破

依旧在线网站爆破

Vigenere Solver | guballa.de

根据提示修改，然后直接将zen2和key2内容填上，运行脚本即可

exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
from hashlib import md5
zen2 = '''
IN THE FACE OF AMBIGUITY, REFUSE THE TEMPTATION TO GUESS.
THERE SHOULD BE ONE-- AND PREFERABLY ONLY ONE --OBVIOUS WAY TO DO IT.
ALTHOUGH THAT WAY MAY NOT BE OBVIOUS AT FIRST UNLESS YOU'RE DUTCH.
NOW IS BETTER THAN NEVER.
ALTHOUGH NEVER IS OFTEN BETTER THAN RIGHT NOW.
IF THE IMPLEMENTATION IS HARD TO EXPLAIN, IT'S A BAD IDEA.
IF THE IMPLEMENTATION IS EASY TO EXPLAIN, IT MAY BE A GOOD IDEA.

'''
key2 ='supersubtitution'
dict1 = {'A': 0, 'B': 1, 'C': 2, 'D': 3, 'E': 4,
         'F': 5, 'G': 6, 'H': 7, 'I': 8, 'J': 9,
         'K': 10, 'L': 11, 'M': 12, 'N': 13, 'O': 14,
         'P': 15, 'Q': 16, 'R': 17, 'S': 18, 'T': 19,
         'U': 20, 'V': 21, 'W': 22, 'X': 23, 'Y': 24, 'Z': 25}

dict2 = {0: 'A', 1: 'B', 2: 'C', 3: 'D', 4: 'E',
         5: 'F', 6: 'G', 7: 'H', 8: 'I', 9: 'J',
         10: 'K', 11: 'L', 12: 'M', 13: 'N', 14: 'O',
         15: 'P', 16: 'Q', 17: 'R', 18: 'S', 19: 'T',
         20: 'U', 21: 'V', 22: 'W', 23: 'X', 24: 'Y', 25: 'Z'}

def generate_key(message, key):
    for i in range(len(message)):
        if message[i].isalpha() == False:
            pass
        else:
            key += message[i]
    return key
def enc2(message, key):
    message = message.upper()
    key = key.upper()
    key_new = generate_key(message, key)
    cipher_text = ''
    i = 0
    for letter in message:
        if letter.isalpha():
            x = (dict1[letter]+dict1[key_new[i]]) % 26
            i += 1
            cipher_text += dict2[x]
        else:
            cipher_text += letter
    return cipher_text
print('enc = \'\'\'' + enc2(zen2, key2)+'\'\'\'')
flag = b'flag{'+md5(zen2.encode()).hexdigest().encode()+b'}'
print(flag)

运行得到

最后flag为

1
flag{8bc383165248f2e45a6910960a61e6a8}

没 e 这能玩？

题目描述：

1
公钥到处乱传，这下大家都能加密了——我不想把 e 告诉大家，只有聪明的宝宝才可以知道

下载附件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
from Crypto.Util.number import *
import random
import sympy
import gmpy2

m = bytes_to_long(b'flag{*****}')

p = getPrime(512)
q = getPrime(512)
r = getPrime(512)
h1 = 1*p + 1*q + 1*r
h2 = 2*p + 3*q + 3*r
h3 = 9*p + 9*q + 6*r
print( "hint_of_pqr=" , h1 , h2 , h3 )

e = getPrime(64)
a_big_prime = getPrime( 512 )
hint = pow(a_big_prime,e,2**512)
print( "big_prime is: " , a_big_prime )
print( "hint is: " , hint )

n = p*q*r
c = pow( m , e , n )
print( "c=" , c )

"""
hint_of_pqr= 31142735238530997044538008977536563192992446755282526163704097825748037157617958329370018716097695151853567914689441893020256819531959835133410539308633497 83244528500940968089139246591338465098116598400576450028712055615289379610182828415628469144649133540240957232351546273836449824638227295064400834828714760 248913032538718194100308575844236838621741774207751338576000867909773931464854644505429950530402814602955352740032796855486666128271187734043696395254816172 
big_prime is:  10340528340717085562564282159472606844701680435801531596688324657589080212070472855731542530063656135954245247693866580524183340161718349111409099098622379
hint is:  1117823254118009923270987314972815939020676918543320218102525712576467969401820234222225849595448982263008967497960941694470967789623418862506421153355571 
c= 999238457633695875390868312148578206874085180328729864031502769160746939370358067645058746087858200698064715590068454781908941878234704745231616472500544299489072907525181954130042610756999951629214871917553371147513692253221476798612645630242018686268404850587754814930425513225710788525640827779311258012457828152843350882248473911459816471101547263923065978812349463656784597759143314955463199850172786928389414560476327593199154879575312027425152329247656310
"""

考点:离散对数

1
e = discrete_log(2**512, hint, big_prime)

exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
from Crypto.Util.number import *
import sympy

# 已知参数
h1 = 31142735238530997044538008977536563192992446755282526163704097825748037157617958329370018716097695151853567914689441893020256819531959835133410539308633497
h2 = 83244528500940968089139246591338465098116598400576450028712055615289379610182828415628469144649133540240957232351546273836449824638227295064400834828714760
h3 = 248913032538718194100308575844236838621741774207751338576000867909773931464854644505429950530402814602955352740032796855486666128271187734043696395254816172
big_prime = 10340528340717085562564282159472606844701680435801531596688324657589080212070472855731542530063656135954245247693866580524183340161718349111409099098622379
hint = 1117823254118009923270987314972815939020676918543320218102525712576467969401820234222225849595448982263008967497960941694470967789623418862506421153355571
c = 999238457633695875390868312148578206874085180328729864031502769160746939370358067645058746087858200698064715590068454781908941878234704745231616472500544299489072907525181954130042610756999951629214871917553371147513692253221476798612645630242018686268404850587754814930425513225710788525640827779311258012457828152843350882248473911459816471101547263923065978812349463656784597759143314955463199850172786928389414560476327593199154879575312027425152329247656310

# 1. 求解p, q, r（通过线性方程组化简）
p = 3 * h1 - h2
r = (9 * h1 - h3) // 3
q = h1 - p - r


# 2. 计算RSA参数
n = p * q * r
phi = (p - 1) * (q - 1) * (r - 1)

# 3. 求解加密指数e（离散对数问题）
e = sympy.discrete_log(2**512, hint, big_prime)
print(f"加密指数e: {e}")

# 4. 计算私钥d
d = inverse(e, phi)
print(f"私钥d: {d}")

# 5. 解密并输出Flag
plaintext = pow(c, d, n)
flag = long_to_bytes(plaintext).decode('utf-8')
print(f"\n[+] 解密成功！Flag为: {flag}")

运行得到

最后flag为

1
flag{th1s_2s_A_rea119_f34ggg}

week4

俱以我之名

题目描述：

1
开启技能后，在天赋生效范围内可部署地面召唤「黄金盟誓」;技能期间可攻击被天赋生效范围阻挡的敌人，攻击时伤害类型变为真实，对 RSA 造成真实伤害。

下载附件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
from Crypto.Util.number import *
from gmpy2 import *
import random

def pad(msg, nbits):
    pad_length = nbits - len(msg) * 8 - 8
    assert pad_length >= 0
    pad = random.getrandbits(pad_length).to_bytes((pad_length + 7) // 8, "big")
    padded_msg = pad[:len(pad)//2] + b"\x00" + msg + pad[len(pad)//2:]

    return padded_msg

def All_in_my_name(p, q):
    #开启三技能<俱以我之名>后，维娜立即在周围八格可部署地面召唤“黄金盟誓(Golden_Oath)”;对RSA造成真实伤害。
    Golden_Oath = (p-114)*(p-514)*(p+114)*(p+514)*(q-1919)*(q-810)*(q+1919)*(q+810)
    x = bytes_to_long(pad(gift, random.randint(bytes_to_long(gift).bit_length(), 512)))
    y = inverse(x, Golden_Oath)
    return y

flag = b'flag{?????}'
gift = b'?????'
assert gift[:3] == b'end'

p = getPrime(512)
q = getPrime(512)
n = p*q
e = 65537
c = pow(bytes_to_long(flag), e,n)

print(f'n = {n}')
print(f'c = {c}')
print(f'All_in_my_name = {All_in_my_name(p, q)}')

'''
n = 141425071303405369267688583480971314815032581405819618511016190023245950842423565456025578726768996255928405749476366742320062773129810617755239412667111588691998380868379955660483185372558973059599254495581547016729479937763213364591413126146102483671385285672028642742654014426993054793378204517214486744679
c = 104575090683421063990494118954150936075812576661759942057772865980855195301985579098801745928083817885393369435101522784385677092942324668770336932487623099755265641877712097977929937088259347596039326198580193524065645826424819334664869152049049342316256537440449958526473368110002271943046726966122355888321
All_in_my_name = 217574365691698773158073738993996550494156171844278669077189161825491226238745356969468902038533922854535578070710976002278064001201980326028443347187697136216041235312192490502479015081704814370278142850634739391445817028960623318683701439854891399013393469200033510113406165952272497324443526299141544564964545937461632903355647411273477731555390580525472533399606416576667193890128726061970653201509841276177937053500663438053151477018183074107182442711656306515049473061426018576304621373895497210927151796054531814746265988174146635716820986208719319296233956243559891444122410388128465897348458862921336261068868678669349968117097659195490792407141240846445006330031546721426459458395606505793093432806236790060342049066284307119546018491926250151057087562126580602631912562103705681810139118673506298916800665912859765635644796622382867334481599049728329203920912683317422430015635091565073203588723830512169316991557606976424732212785533550238950903858852917097354055547392337744369560947616517041907362337902584102983344969307971888314998036201926257375424706901999793914432814775462333942995267009264203787170147555384279151485485660683109778282239772043598128219664150933315760352868905799949049880756509591090387073778041
'''

考点:维纳攻击和连分数

参考文章

en.wikipedia.org

文章列表 | NSSCTF

求Golden_Oath，以及pq关系

exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
from Crypto.Util.number import *
from gmpy2 import *
import random

n = 141425071303405369267688583480971314815032581405819618511016190023245950842423565456025578726768996255928405749476366742320062773129810617755239412667111588691998380868379955660483185372558973059599254495581547016729479937763213364591413126146102483671385285672028642742654014426993054793378204517214486744679
c = 104575090683421063990494118954150936075812576661759942057772865980855195301985579098801745928083817885393369435101522784385677092942324668770336932487623099755265641877712097977929937088259347596039326198580193524065645826424819334664869152049049342316256537440449958526473368110002271943046726966122355888321
y = 217574365691698773158073738993996550494156171844278669077189161825491226238745356969468902038533922854535578070710976002278064001201980326028443347187697136216041235312192490502479015081704814370278142850634739391445817028960623318683701439854891399013393469200033510113406165952272497324443526299141544564964545937461632903355647411273477731555390580525472533399606416576667193890128726061970653201509841276177937053500663438053151477018183074107182442711656306515049473061426018576304621373895497210927151796054531814746265988174146635716820986208719319296233956243559891444122410388128465897348458862921336261068868678669349968117097659195490792407141240846445006330031546721426459458395606505793093432806236790060342049066284307119546018491926250151057087562126580602631912562103705681810139118673506298916800665912859765635644796622382867334481599049728329203920912683317422430015635091565073203588723830512169316991557606976424732212785533550238950903858852917097354055547392337744369560947616517041907362337902584102983344969307971888314998036201926257375424706901999793914432814775462333942995267009264203787170147555384279151485485660683109778282239772043598128219664150933315760352868905799949049880756509591090387073778041
e = 65537

class ContinuedFraction():
    def __init__(self, numerator, denumerator):
        self.numberlist = []
        self.fractionlist = []
        self.GenerateNumberList(numerator, denumerator)
        self.GenerateFractionList()

    def GenerateNumberList(self, numerator, denumerator):
        while numerator != 1:
            quotient = numerator // denumerator
            remainder = numerator % denumerator
            self.numberlist.append(quotient)
            numerator = denumerator
            denumerator = remainder

    def GenerateFractionList(self):
        self.fractionlist.append([self.numberlist[0], 1])
        for i in range(1, len(self.numberlist)):
            numerator = self.numberlist[i]
            denumerator = 1
            for j in range(i):
                temp = numerator
                numerator = denumerator + numerator * self.numberlist[i - j - 1]
                denumerator = temp
            self.fractionlist.append([numerator, denumerator])

n = pow(n,4)
a = ContinuedFraction(y, n)
for k, x in a.fractionlist:
    # 判断哪一个是我们所需的 x
    if b'end' in long_to_bytes(x):
        print(x)
        print(k)
        break

print(long_to_bytes(x))
Golden_Oath = (x*y-1)//k
print(Golden_Oath)

'''
103697213497220650500739251621743955651854455782387759691953279488676501281257640431561
56398712132783063027132828918468670442692437484816382768162819797891220782528221182512
b'5`\xf4\xf6t\xa3\x00end1n9_A_G2@nd_Ov3RTu2e\x1c\x13"H\x0f\xc9'
#400042032831098007958224589201074030167511216235146696966889080122265111949126155016295896501799032251334875101500882585261911204171467951139573150807043239564581043145433814155757093989016940205116328236031283789686099217459678429270939065783626769903068201144816933538226628329294355184200590029028565011348654002192085571172863125467318356642528249715812871925525776008917314884490518613080652875623759460663908309369135829140204137773254011408135516737187092812588388209697036416805176286184831779945910125467423823737934475944632379524991238593952097013985394648562259886597816452815669024660257170465154297959999722533255899489096196292778430386116108069053440749172609798098777046509743030019115282253351905670418760503352277616008654327326851761671410084489662135479597061419403235762755010286075975241013273964842915146756571330207605591193457296347769260777032489271278979332616929093357929916558230665466587125254822846466292980360420737307459205352964255972268278992730637939153686420457279334894980200862788513296786385507282999530973028293157179873999483225505784146175328159014143540959190522315340971608002638786511995717564457749873410017343184395040614025573440462522210939180555090227730875845671821586191943346000
'''

运行得到

使用 sympy库解方程

exp：

1
2
3
4
5
6
7
8
9
10
11
12
Golden_Oath = 400042032831098007958224589201074030167511216235146696966889080122265111949126155016295896501799032251334875101500882585261911204171467951139573150807043239564581043145433814155757093989016940205116328236031283789686099217459678429270939065783626769903068201144816933538226628329294355184200590029028565011348654002192085571172863125467318356642528249715812871925525776008917314884490518613080652875623759460663908309369135829140204137773254011408135516737187092812588388209697036416805176286184831779945910125467423823737934475944632379524991238593952097013985394648562259886597816452815669024660257170465154297959999722533255899489096196292778430386116108069053440749172609798098777046509743030019115282253351905670418760503352277616008654327326851761671410084489662135479597061419403235762755010286075975241013273964842915146756571330207605591193457296347769260777032489271278979332616929093357929916558230665466587125254822846466292980360420737307459205352964255972268278992730637939153686420457279334894980200862788513296786385507282999530973028293157179873999483225505784146175328159014143540959190522315340971608002638786511995717564457749873410017343184395040614025573440462522210939180555090227730875845671821586191943346000
from sympy import symbols, Eq, solve
n = 141425071303405369267688583480971314815032581405819618511016190023245950842423565456025578726768996255928405749476366742320062773129810617755239412667111588691998380868379955660483185372558973059599254495581547016729479937763213364591413126146102483671385285672028642742654014426993054793378204517214486744679
p, q = symbols('p q')
equation1 = Eq(p * q, n)
equation2 = Eq((p-114)*(p-514)*(p+114)*(p+514)*(q-1919)*(q-810)*(q+1919)*(q+810), Golden_Oath)
solutions = solve((equation1, equation2), (p, q))
print(f"p 和 q 的解: {solutions}")

'''
p 和 q 的解: [(-11256874906034337229658272553494271626180719204801621165552253304119314454014247481847595578004383239651599038196432752043642616511808644606155091511313329, -12563439896413287507369191021540890661182794010085857062984791988214078294298809633469029528754549607502031091193150571585844351836163514784874848514208151), (11256874906034337229658272553494271626180719204801621165552253304119314454014247481847595578004383239651599038196432752043642616511808644606155091511313329, 12563439896413287507369191021540890661182794010085857062984791988214078294298809633469029528754549607502031091193150571585844351836163514784874848514208151)]
'''

运行得到

得到p，q，常规rsa解密即可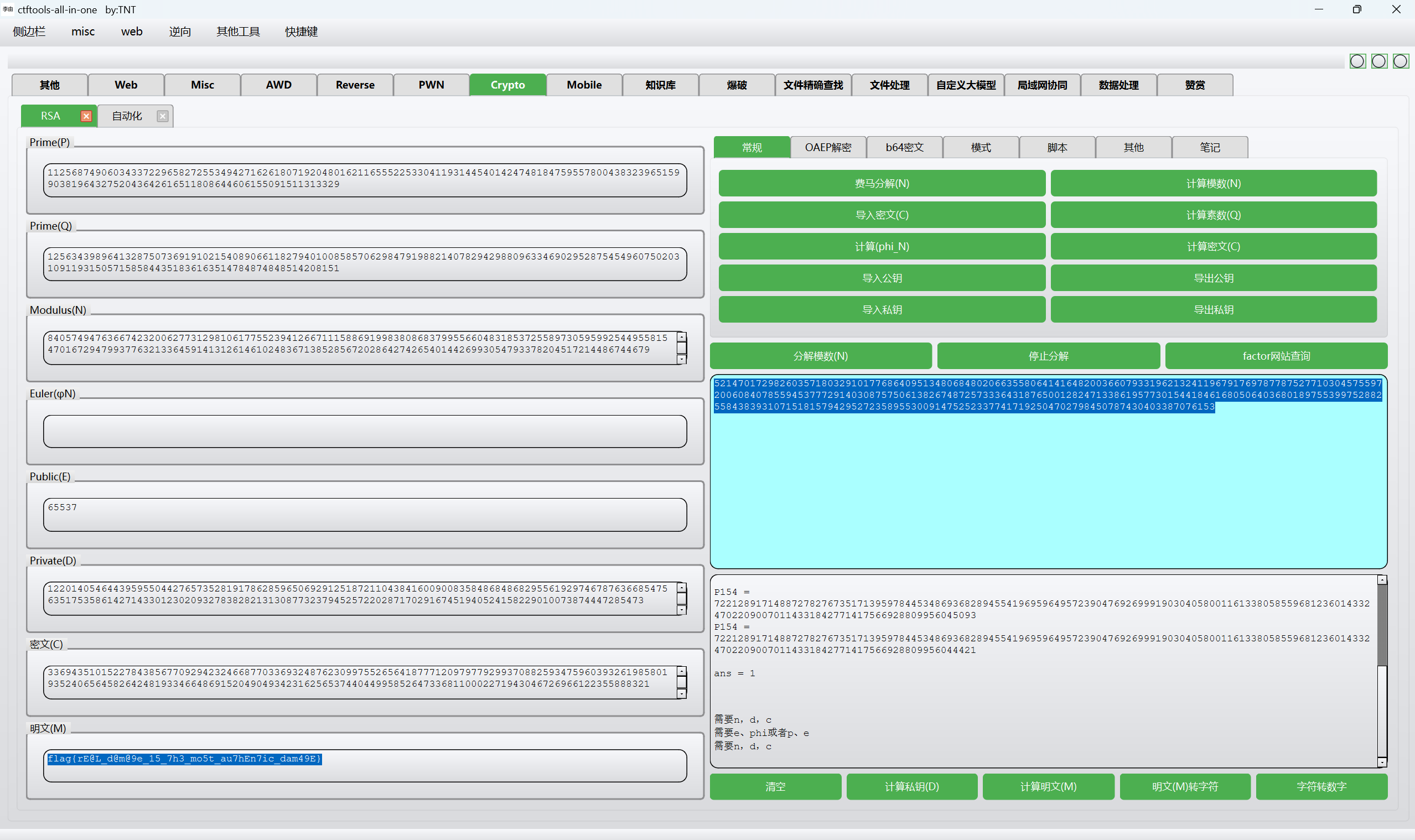

最后flag为

1
flag{rE@L_d@m@9e_15_7h3_mo5t_au7hEn7ic_dam49E}

圣石匕首

题目描述：

1
贤者拿到了一段 exp，运行它即可快速解开谜题，获取 flag. 但是他好像没有见过这种代码……

下载附件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
import gmpy2
beta=0.37
delta=0.01
n=round((1-2*beta-2*delta)/((1-beta)^2-2*delta-beta),6)
e= 3668637434348843171145584606519031375027610199908169273169275927238735031431533260375377791001464799116453803408104076615710166171199990283470548282669948353598733020244755959461974603778630346457439345913209321194112256348302765254052193562603687450740346132207444615610078198488883539133291840346099727880587092122957231085658576850601488737629051252914095889313671875244094452330062619943781809984690384476868543570724769198985172300665613239047649089399919032152539462701309393130614829962670866062380816370571057536421400102100259975636785825540933280194583888638501981649650640939392658268133881679239293596283
N= 9748523098652101859947730585916490335896800943242955095820326993765071194474558998322598145898741779502734772138283011560029368500998354183150180904846368209977332058847768859238711047784703104535311583123388923571789764758869419482184613566672922481672444028753365755071127320541645016370072493604532087980626825687519083734367691341907014061379844209864141989961751681235215504772582878202048494707090104738899927036896915997556102574747166491969027546256022019959716418675672979328622656831990050058120299353807110233202113906317969377201045402271911946244076903611612303290556012512559696538977841061277173754331
c= 5374936627659221745209010619827617207565185520404653329184605916859755641352457088986635357806048863755173540232471505333583684733535121482637476692432365062808450583470788320547816186936317927449796090525477205337038591439577855884910604383190932340306435201976465543731935147881754136301375206828970248293731391543905441514528959500307972606931927112031018356411970001312995489429650903529877904694901310020882390008248466887950986326522740278880600110217817950511478637493101027659292006016454642135508207492151610829525082829566392116546434101694921106423469015683277992978077101831969525458693031031468092418427
n=int(n+1)
#print(n)
m=int(n*(1-beta))
X=int(pow(N,delta))
Y=int(pow(N,delta+beta))
Z.<x,y>=ZZ[]
L=Matrix(ZZ,n,n)
f=e*x-y
for i in range(n):
    g=list(N^max(0,m-i)*x^(n-1-i)*f^i)
    for j in range(len(g)):
        L[i,j]=g[j][0]*X^(n-1-j)*Y^j
L=L.LLL()[0]
coeff=[]
for i in range(n):
    coeff.append((L[i]//(X^(n-1-i)*Y^i),'x'+'**'+str(n-1-i)+'*y'+'**'+str(i)))
s=''
for i in range(len(coeff)):
    s+=str(coeff[i][0])+'*'+coeff[i][1]+'+'
f=eval(s[:-1])
factored_f = f.factor()
first_polynomial = factored_f[0][0]
first_coefficient = first_polynomial.coefficients()[0]
k = first_coefficient + 1
dp = first_polynomial.coefficients()[1]
p=(e*dp-1)//k+1
q=N//p
phi=(p-1)*(q-1)
d=gmpy2.invert(e,phi)
m=pow(c,d,N)
print(bytes.fromhex(hex(m)[2:]))

考点:sagemath使用

直接sage运行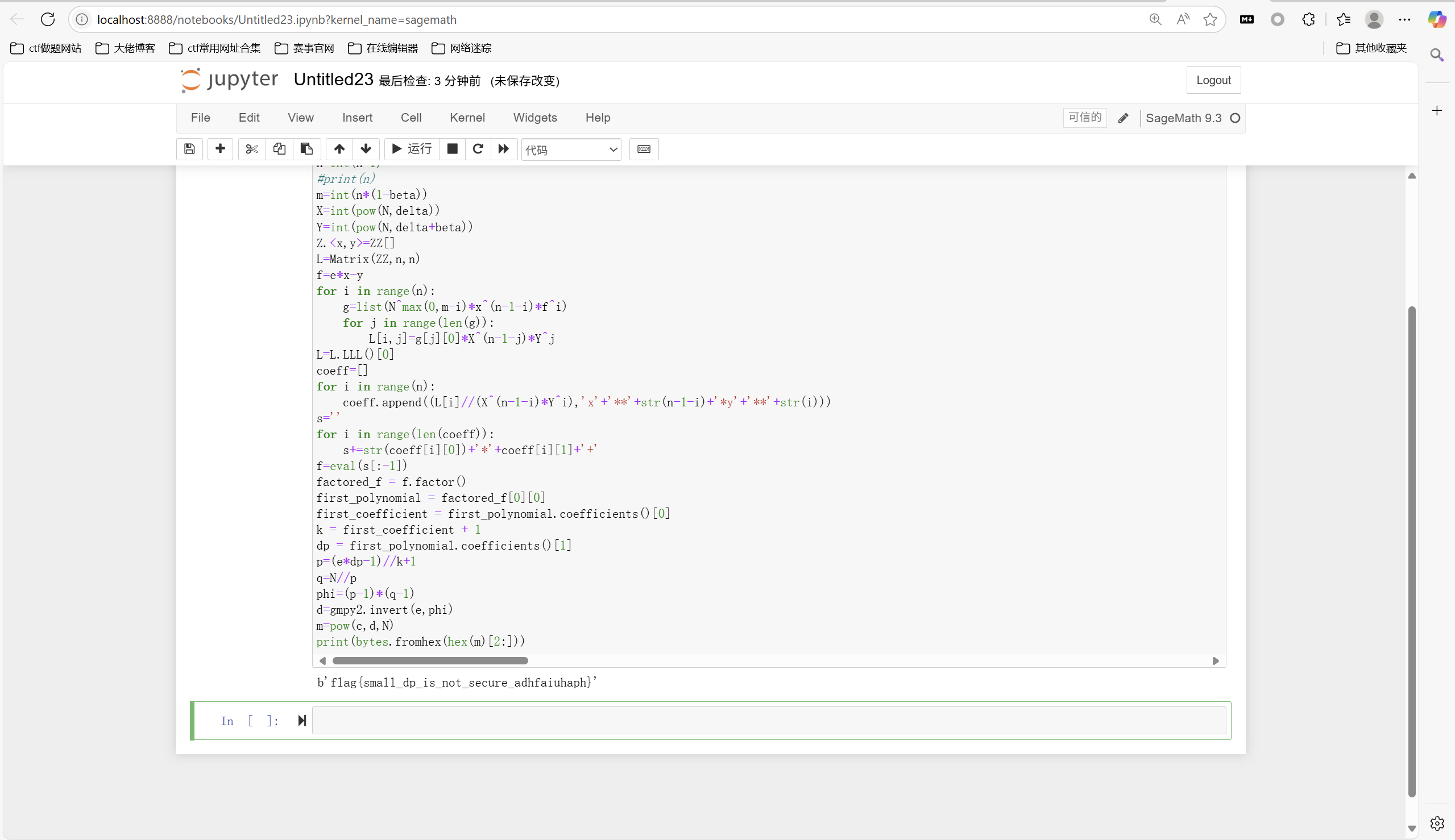

最后flag为

1
flag{small_dp_is_not_secure_adhfaiuhaph}

欧拉欧拉！！

题目描述：

1
完啦！q 被 ≪大运撞进二进制世界，它能否和 p 联手一起，拿到 φ，回到十进制世界

下载附件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
from Crypto.Util.number import *

flag = b'flag{*********}'
m = bytes_to_long(flag)


def get_prime(bits):
    while True:
        p = getPrime(bits)
        x = (1 << bits) - 1 ^ p
        for i in range(-10, 11):
            if isPrime(x + i):
                return p, x + i, i


p, q, i = get_prime(512)
n = p * q
e = 65537
c = pow(m, e, n)

print("c =", c)
print("n =", n)
print("i =", i)
'''
c = 14859652090105683079145454585893160422247900801288656111826569181159038438427898859238993694117308678150258749913747829849091269373672489350727536945889312021893859587868138786640133976196803958879602927438349289325983895357127086714561807181967380062187404628829595784290171905916316214021661729616120643997
n = 18104347461003907895610914021247683508445228187648940019610703551961828343286923443588324205257353157349226965840638901792059481287140055747874675375786201782262247550663098932351593199099796736521757473187142907551498526346132033381442243277945568526912391580431142769526917165011590824127172120180838162091
i = -3
'''

考点:二进制加法，间接求欧拉函数

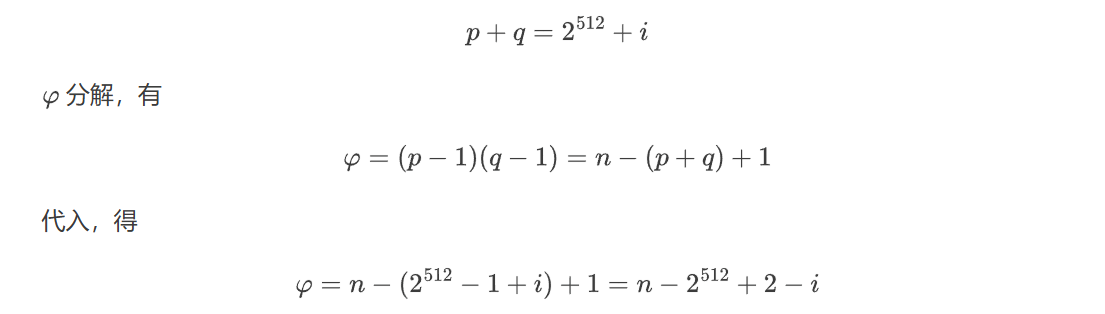
exp:

1
2
3
4
5
6
7
8
9
10
from Crypto.Util.number import *
c = 14859652090105683079145454585893160422247900801288656111826569181159038438427898859238993694117308678150258749913747829849091269373672489350727536945889312021893859587868138786640133976196803958879602927438349289325983895357127086714561807181967380062187404628829595784290171905916316214021661729616120643997
n = 18104347461003907895610914021247683508445228187648940019610703551961828343286923443588324205257353157349226965840638901792059481287140055747874675375786201782262247550663098932351593199099796736521757473187142907551498526346132033381442243277945568526912391580431142769526917165011590824127172120180838162091
i = -3
e = 65537

phi = n - 2**512 + 2 - i
d = inverse(e, phi)
m = pow(c, d, n)
print(long_to_bytes(m))

运行得到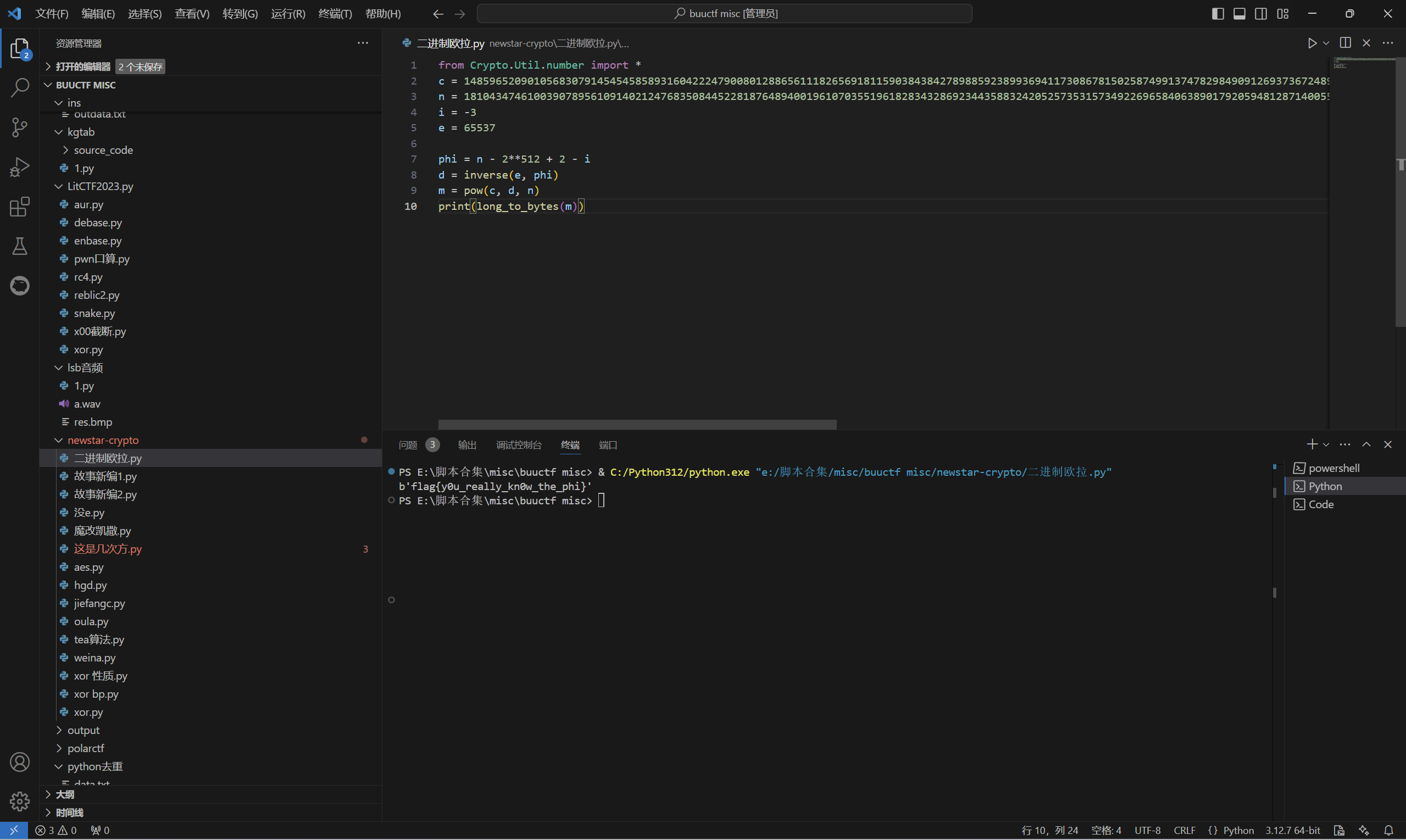

最后flag为

1
flag{y0u_really_kn0w_the_phi}

week5

RSA? cmd5!

题目描述：

1
2
3
4
5
应该都了解 RSA 解密原理了吧？

Alice: 你把服务器密码用 RSA 加密给我发过来吧，记得带上签名

Bob: 好麻烦，还要签名，算了，直接 MD5 签名一下就好了吧！

下载附件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
from Crypto.Util.number import *
from gmpy2 import *
import hashlib

# 什么？你说你用md5给rsa签名了？！

m = '*******'
assert len(m) == 7
flag = 'flag{th1s_1s_my_k3y:' + m + '0x' + hashlib.sha256(m.encode()).hexdigest() + '}'

p = getStrongPrime(512)
q = getStrongPrime(512)
n = p * q
e = 65537
phi = (p - 1) * (q - 1)
d = inverse(e, phi)


def get_MD5(m0):
    import hashlib
    md5_object = hashlib.md5(m0.encode())
    md5_result = md5_object.hexdigest()
    return md5_result


def get_s(m0, d0, n0):
    hm0 = get_MD5(m0)
    hm1 = bytes_to_long(hm0.encode())
    s0 = pow(hm1, d0, n0)
    return s0


def rsa_encode(m0, e0, n0):
    m1 = bytes_to_long(m0.encode())
    c0 = pow(m1, e0, n0)
    return c0


def get_flag(m0):  # 请用这个函数来转m得到flag
    import hashlib
    flag = 'flag{th1s_1s_my_k3y:' + m0 + '0x' + hashlib.sha256(m0.encode()).hexdigest() + '}'
    print(flag)


s = get_s(m, d, n)
c = rsa_encode(flag, e, n)

print("密文c =", c)
print("签名s =", s)
print("公钥[n,e] =", [n, e])

'''
密文c = 119084320846787611587774426118526847905825678869032529318497425064970463356147909835330423466179802531093233559613714033492951177656433798856482195873924140269461792479008703758436687940228268475598134411304167494814557384094637387369282900460926092035234233538644197114822992825439656673482850515654334379332
签名s = 5461514893126669960233658468203682813465911805334274462134892270260355037191167357098405392972668890146716863374229152116784218921275571185229135409696720018765930919309887205786492284716906060670649040459662723215737124829497658722113929054827469554157634284671989682162929417551313954916635460603628116503
公钥[n,e] = [139458221347981983099030378716991183653410063401398496859351212711302933950230621243347114295539950275542983665063430931475751013491128583801570410029527087462464558398730501041018349125941967135719526654701663270142483830687281477000567117071676521061576952568958398421029292366101543468414270793284704549051, 65537]
'''

考点:RSA MD5数字签名

RSA 数字签名 - CTF Wiki

exp:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
from Crypto.Util.number import *
from gmpy2 import *
import hashlib

# 已知参数
c = 119084320846787611587774426118526847905825678869032529318497425064970463356147909835330423466179802531093233559613714033492951177656433798856482195873924140269461792479008703758436687940228268475598134411304167494814557384094637387369282900460926092035234233538644197114822992825439656673482850515654334379332
s = 5461514893126669960233658468203682813465911805334274462134892270260355037191167357098405392972668890146716863374229152116784218921275571185229135409696720018765930919309887205786492284716906060670649040459662723215737124829497658722113929054827469554157634284671989682162929417551313954916635460603628116503
n = 139458221347981983099030378716991183653410063401398496859351212711302933950230621243347114295539950275542983665063430931475751013491128583801570410029527087462464558398730501041018349125941967135719526654701663270142483830687281477000567117071676521061576952568958398421029292366101543468414270793284704549051
e = 65537

# 步骤1：恢复MD5哈希值
hm0 = pow(s, e, n)  # 使用RSA验证过程恢复哈希值
md5_hash = long_to_bytes(int(hm0))
print(f"恢复的MD5哈希值: {md5_hash.hex()}")

# 步骤2：构建flag（已知m0='adm0n12'）
m0 = 'adm0n12'
flag = 'flag{th1s_1s_my_k3y:' + m0 + '0x' + hashlib.sha256(m0.encode()).hexdigest() + '}'
print(f"Flag: {flag}")

# 验证步骤：检查md5_hash是否匹配
md5_verify = hashlib.md5(m0.encode()).hexdigest()
print(f"m0的MD5哈希值: {md5_verify}")
print(f"哈希值匹配: {md5_verify == md5_hash.hex()}")

运行得到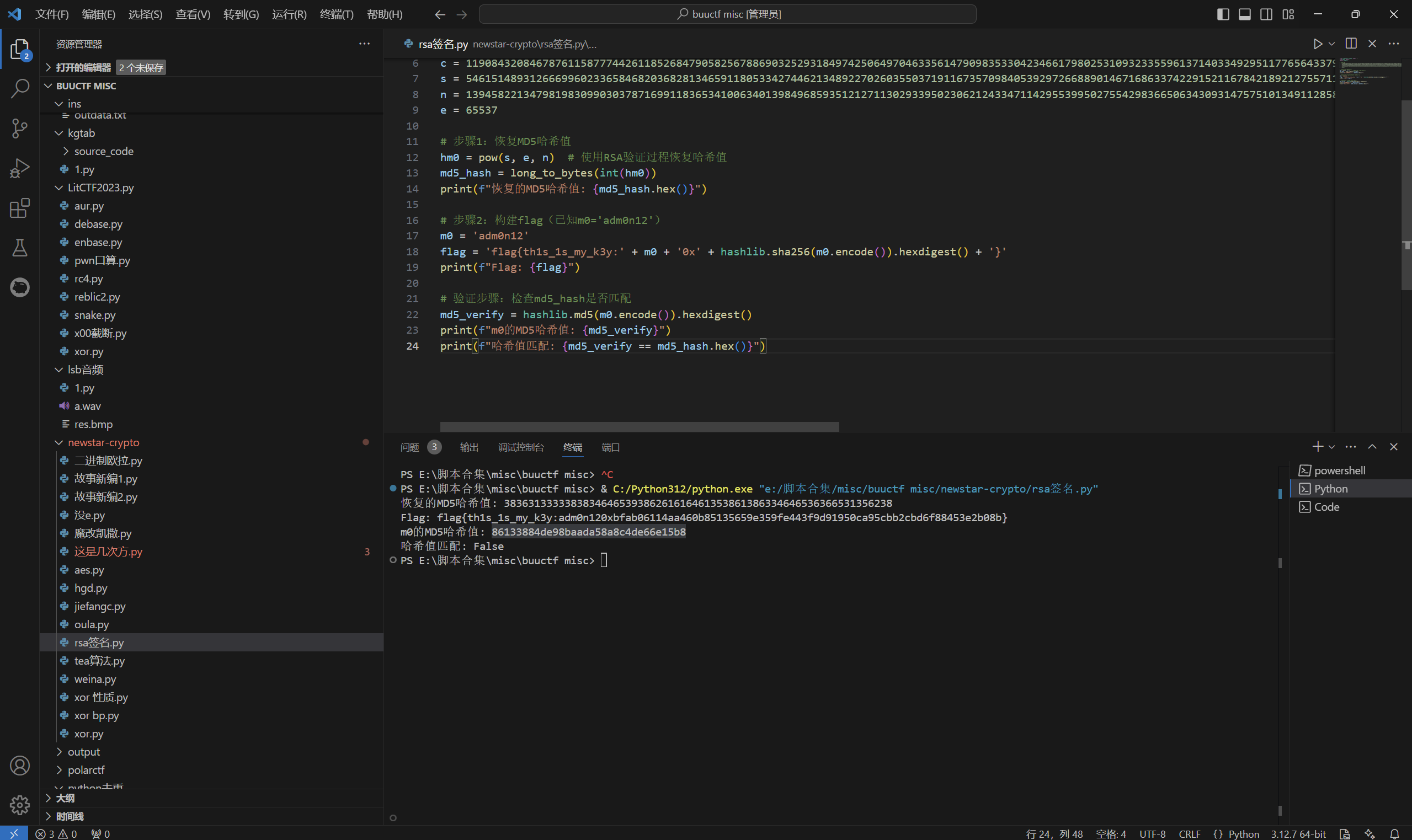

最后flag为

1
flag{th1s_1s_my_k3y:adm0n120xbfab06114aa460b85135659e359fe443f9d91950ca95cbb2cbd6f88453e2b08b}

easy_ecc

题目描述：

1
简单的椭圆曲线密码入门

下载附件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
from Crypto.Util.number import * # type: ignore
from secret import flag

p = 64408890408990977312449920805352688472706861581336743385477748208693864804529
a = 111430905433526442875199303277188510507615671079377406541731212384727808735043
b = 89198454229925288228295769729512965517404638795380570071386449796440992672131
E = EllipticCurve(GF(p),[a,b])
m = E.random_point()
G = E.random_point()
k = 86388708736702446338970388622357740462258632504448854088010402300997950626097
K = k * G
r = getPrime(256)
c1 = m + r * K
c2 = r * G
c_left =bytes_to_long(flag[:len(flag)//2]) * m[0]
c_right = bytes_to_long(flag[len(flag)//2:]) * m[1]


print(f"c1 = {c1}")
print(f"c2 = {c2}")
print(f"cipher_left = {c_left}")
print(f"cipher_right = {c_right}")


'''
c1 = (10968743933204598092696133780775439201414778610710138014434989682840359444219 : 50103014985350991132553587845849427708725164924911977563743169106436852927878 : 1)
c2 = (16867464324078683910705186791465451317548022113044260821414766837123655851895 : 35017929439600128416871870160299373917483006878637442291141472473285240957511 : 1)
c_left = 15994601655318787407246474983001154806876869424718464381078733967623659362582
c_right = 3289163848384516328785319206783144958342012136997423465408554351179699716569
'''

考点:ECC

exp:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
from Crypto.Util.number import long_to_bytes

p = 64408890408990977312449920805352688472706861581336743385477748208693864804529
a = 111430905433526442875199303277188510507615671079377406541731212384727808735043
b = 89198454229925288228295769729512965517404638795380570071386449796440992672131
k = 86388708736702446338970388622357740462258632504448854088010402300997950626097

c1_x = 10968743933204598092696133780775439201414778610710138014434989682840359444219
c1_y = 50103014985350991132553587845849427708725164924911977563743169106436852927878
c2_x = 16867464324078683910705186791465451317548022113044260821414766837123655851895
c2_y = 35017929439600128416871870160299373917483006878637442291141472473285240957511

c_left = 15994601655318787407246474983001154806876869424718464381078733967623659362582
c_right = 3289163848384516328785319206783144958342012136997423465408554351179699716569

# Define the elliptic curve
E = EllipticCurve(GF(p), [a, b])
c1 = E(c1_x, c1_y)
c2 = E(c2_x, c2_y)

# Compute m = c1 - k * c2
m = c1 - k * c2
m0 = m[0]
m1 = m[1]

# Compute modular inverses
m0_inv = inverse_mod(int(m0), p)
m1_inv = inverse_mod(int(m1), p)

# Recover flag halves
flag_left_int = (c_left * m0_inv) % p
flag_right_int = (c_right * m1_inv) % p

# Convert to bytes
flag_left = long_to_bytes(flag_left_int)
flag_right = long_to_bytes(flag_right_int)

flag = flag_left + flag_right
print(flag.decode())

运行得到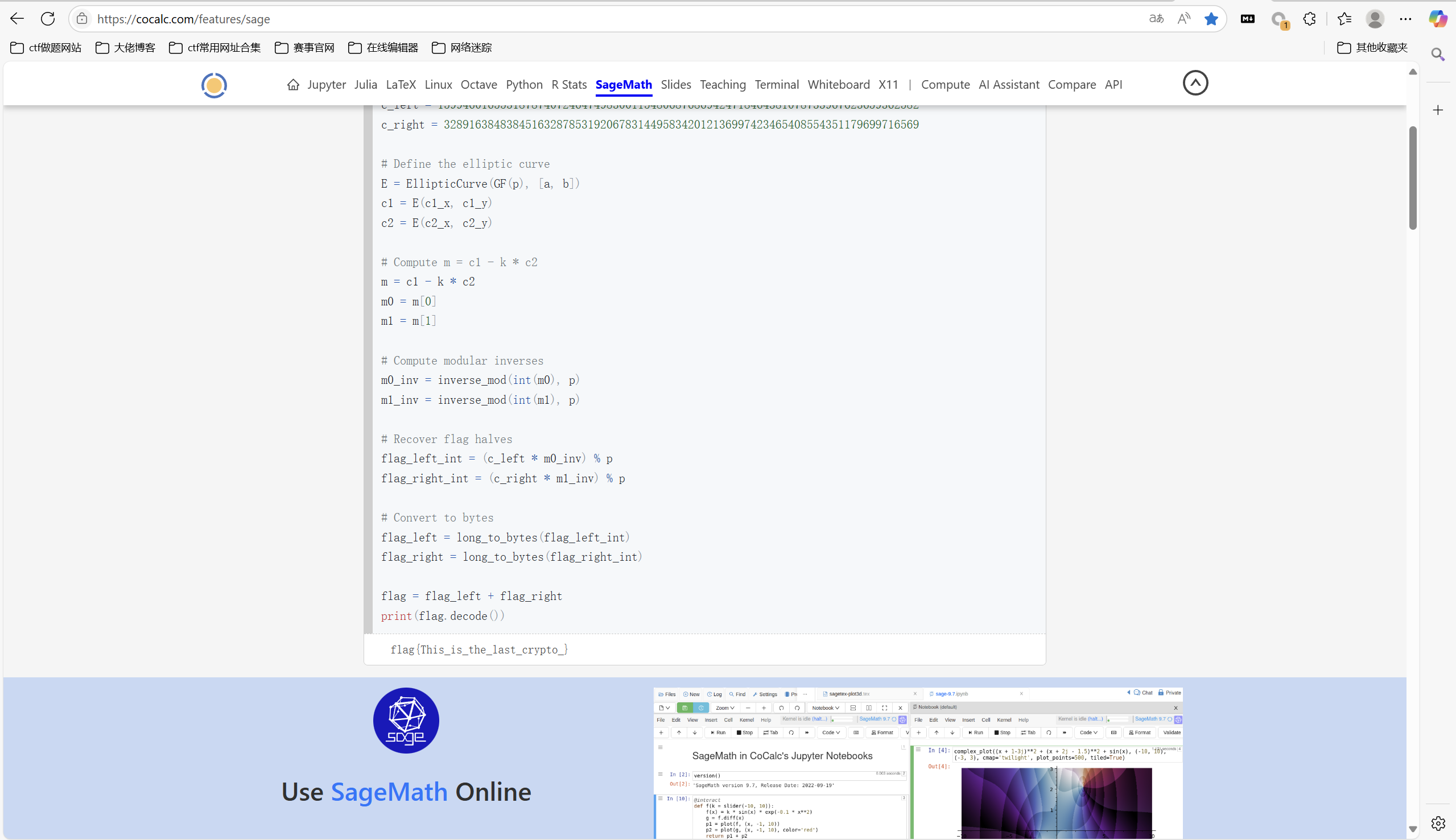

最后flag为

1
flag{This_is_the_last_crypto_}

学以致用

题目描述：

1
2
3
4
5
6
7
8
9
—— 帮帮我，sagemath 先生，TAT

—— NewStar，我来助你！

http://users.ece.cmu.edu/~reiter/papers/1996/Eurocrypt.pdf

https://doc.sagemath.org/html/en/reference/

24 新生 NewStar 同学，考验你自学与运用能力的时刻到了！（不加难度，最后一周给大家放松一下了）

下载附件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import random
from Crypto.Util.number import *

def pad(msg, nbits):
    # pad了一下，仔细看看，别好不容易解出来了却没看到flag👼
    pad_length = nbits - len(msg) * 8 - 16
    assert pad_length >= 0
    pad = random.getrandbits(pad_length).to_bytes((pad_length + 7) // 8, "big")
    return pad[:len(pad)//2] + b"*" + msg + b"*" + pad[len(pad)//2:]

if __name__ == '__main__':
    p = getPrime(1024)
    q = getPrime(1024)
    n = p*q
    e = 3
    Nbits = 2048
    flag = b'flag{?????}'
    gift = b'GoOd_byE_nEw_5t@r'
    
    flag1 = bytes_to_long(pad(flag[:len(flag)//2], Nbits-1))
    flag2 = bytes_to_long(pad(flag[len(flag)//2:], Nbits-1))

    print('n =',n)
    print('c1 =', pow(flag1, e, n))
    print('c2 =', pow(flag2, e, n))
    print('c3 =', pow(flag1 + flag2 + bytes_to_long(gift), e, n))

'''
n = 17072342544150714171879132077494975311237876365187751353863158074020024719122755004761547735987417065592254800869192615807192722193500063611855839293567948232939959753821265552288663615847715716482887552271575844394350597695771100384136647573934496089812758071894172682439278191678102960768874456521879228612030147515967603129172838399997929502420254427798644285909855414606857035622716853274887875327854429218889083561315575947852542496274004905526475639809955792541187225767181054156589100604740904889686749740630242668885218256352895323426975708439512538106136364251265896292820030381364013059573189847777297569447
c1 = 8101607280875746172766350224846108949565038929638360896232937975003150339090901182469578468557951846695946788093600030667125114278821199071782965501023811374181199570231982146140558093531414276709503788909827053368206185816004954186722115752214445121933300663507795347827581212475501366473409732970429363451582182754416452300394502623461416323078625518733218381660019606631159370121924340238446442870526675388637840247597153414432589505667533462640554984002009801576552636432097311654946821118444391557368410974979376926427631136361612166670672126393485023374083079458502529640435635667010258110833498681992307452573
c2 = 14065316670254822235992102489645154264346717769174145550276846121970418622727279704820311564029018067692096462028836081822787148419633716320984336571241963063899868344606864544582504200779938815500203097282542495029462627888080005688408399148971228321637101593575245562307799087481654331283466914448740771421597528473762480363235531826325289856465115044393153437766069365345615753845871983173987642746989559569021189014927911398163825342784515926151087560415374622389991673648463353143338452444851518310480115818005343166067775633021475978188567581820594153290828348099804042221601767330439504722881619147742710013878
c3 = 8094336015065392504689373372598739049074197380146388624166244791783464194652108498071001125262374720857829973449322589841225625661419126346483855290185428811872962549590383450801103516360026351074061702370835578483728260907424050069246549733800397741622131857548326468990903316013060783020272342924805005685309618377803255796096301560780471163963183261626005358125719453918037250566140850975432188309997670739064455030447411193814358481031511873409200036846039285091561677264719855466015739963580639810265153141785946270781617266125399412714450669028767459800001425248072586059267446605354915948603996477113109045600
'''

考点:groebner_basis()

3个方程2个未知数，度又很低，直接求groebner_basis

exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
# sage
from Crypto.Util.number import long_to_bytes, bytes_to_long

n = 17072342544150714171879132077494975311237876365187751353863158074020024719122755004761547735987417065592254800869192615807192722193500063611855839293567948232939959753821265552288663615847715716482887552271575844394350597695771100384136647573934496089812758071894172682439278191678102960768874456521879228612030147515967603129172838399997929502420254427798644285909855414606857035622716853274887875327854429218889083561315575947852542496274004905526475639809955792541187225767181054156589100604740904889686749740630242668885218256352895323426975708439512538106136364251265896292820030381364013059573189847777297569447
c1 = 8101607280875746172766350224846108949565038929638360896232937975003150339090901182469578468557951846695946788093600030667125114278821199071782965501023811374181199570231982146140558093531414276709503788909827053368206185816004954186722115752214445121933300663507795347827581212475501366473409732970429363451582182754416452300394502623461416323078625518733218381660019606631159370121924340238446442870526675388637840247597153414432589505667533462640554984002009801576552636432097311654946821118444391557368410974979376926427631136361612166670672126393485023374083079458502529640435635667010258110833498681992307452573
c2 = 14065316670254822235992102489645154264346717769174145550276846121970418622727279704820311564029018067692096462028836081822787148419633716320984336571241963063899868344606864544582504200779938815500203097282542495029462627888080005688408399148971228321637101593575245562307799087481654331283466914448740771421597528473762480363235531826325289856465115044393153437766069365345615753845871983173987642746989559569021189014927911398163825342784515926151087560415374622389991673648463353143338452444851518310480115818005343166067775633021475978188567581820594153290828348099804042221601767330439504722881619147742710013878
c3 = 8094336015065392504689373372598739049074197380146388624166244791783464194652108498071001125262374720857829973449322589841225625661419126346483855290185428811872962549590383450801103516360026351074061702370835578483728260907424050069246549733800397741622131857548326468990903316013060783020272342924805005685309618377803255796096301560780471163963183261626005358125719453918037250566140850975432188309997670739064455030447411193814358481031511873409200036846039285091561677264719855466015739963580639810265153141785946270781617266125399412714450669028767459800001425248072586059267446605354915948603996477113109045600
gift = b'GoOd_byE_nEw_5t@r'

x, y = PolynomialRing(Zmod(n), 'x, y').gens()
f1 = x**3 - c1
f2 = y**3 - c2
f3 = (x + y + bytes_to_long(gift))**3 - c3

gb = Ideal(f1, f2, f3).groebner_basis()
f1, f2 = gb    # 返回一个多项式

flag1 = int(-f1.coefficients()[1])    # 取负是为了求出m，因为上面多项式是x减去我们所求

flag2 = int(-f2.coefficients()[1])
print(flag1)
# 出题的时候加了给pad，大家得注意一下，flag在一堆trash中间，别做出了却没看见flag
print((long_to_bytes(flag1)).split(b'*')[2]+(long_to_bytes(flag2).split(b'*')[1]))

运行得到

最后flag为

1
flag{W1Sh_you_Bec0me_an_excelL3nt_crypt0G2@pher}

格格你好棒

题目描述：

1
连 n 都没有给的 RSA？！！！快去求救格哥哥！

下载附件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
from Crypto.Util.number import *
import random

flag = b'******'
m = bytes_to_long(flag)

a = getPrime(1024)
b = getPrime(1536)

p = getPrime(512)
q = getPrime(512)
r = random.randint(2**8, 2**9)
assert ((p+2*r) * 3*a + q) % b < 70

c = pow(m, 0x10001, p*q)

print(f'c =', c)
print(f'a =', a)
print(f'b =', b)

'''
c = 75671328500214475056134178451562126288749723392201857886683373274067151096013132141603734799638338446362190819013087028001291030248155587072037662295281180020447012070607162188511029753418358484745755426924178896079516327814868477319474776976247356213687362358286132623490797882893844885783660230132191533753
a = 99829685822966835958276444400403912618712610766908190376329921929407293564120124118477505585269077089315008380226830398574538050051718929826764449053677947419802792746249036134153510802052121734874555372027104653797402194532536147269634489642315951326590902954822775489385580372064589623985262480894316345817
b = 2384473327543107262477269141248562917518395867365960655318142892515553817531439357316940290934095375085624218120779709239118821966188906173260307431682367028597612973683887401344727494920856592020970209197406324257478251502340099862501536622889923455273016634520507179507645734423860654584092233709560055803703801064153206431244982586989154685048854436858839309457140702847482240801158808592615931654823643778920270174913454238149949865979522520566288822366419746
'''

考点:格攻击

参考

【CTF-Crypto】格密码基础（例题较多，非常适合入门！）_ctf crypto-CSDN博客

线性代数基础——矩阵和矩阵的乘法 - 知乎

exp:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
from gmpy2 import *
from Crypto.Util.number import *

c = 63970090307730335877809721304200883550049640814796584855311919788444862517887223732986595675409088426370045912297203884697715744287109423956446588104144896948474600924252971426757693149049788176140093762669257572818136268391076675502412382985137721246839664247241033867414491199483652292036165169353341736721
a = 169095591032842107903100075180638676605851796444162152675549552436872904263319011471312171874748357621716550291723406808357475877569622382251716493461335948233920131882151228308789748286370580144669281233868187101339909767205887609164975015547772498904502805235278789412044800177551190013789791754504529931231
b = 6064645365981235887306179215270851271718801644429108711725310294864007556801445216060166346337708059041073442260127725535139356989204300545757168654885686344461282796094266688090445897296901297377920786192865778222921548386038058555872765953356732109313734205459623312689902913019046944089470201948948652890006944620407534229412159275346491001935499731177063675134035072472112134333424000794637616785944210359606751334132126595044554089452160862222153579096125950

mat = [[b, 0], [3*a, 1]]
M = Matrix(ZZ, mat)
v = M.LLL()[0]
qq = v[0]
pp = v[1]

print(f"pp = {pp}")
print(f"qq = {qq}")

运行得到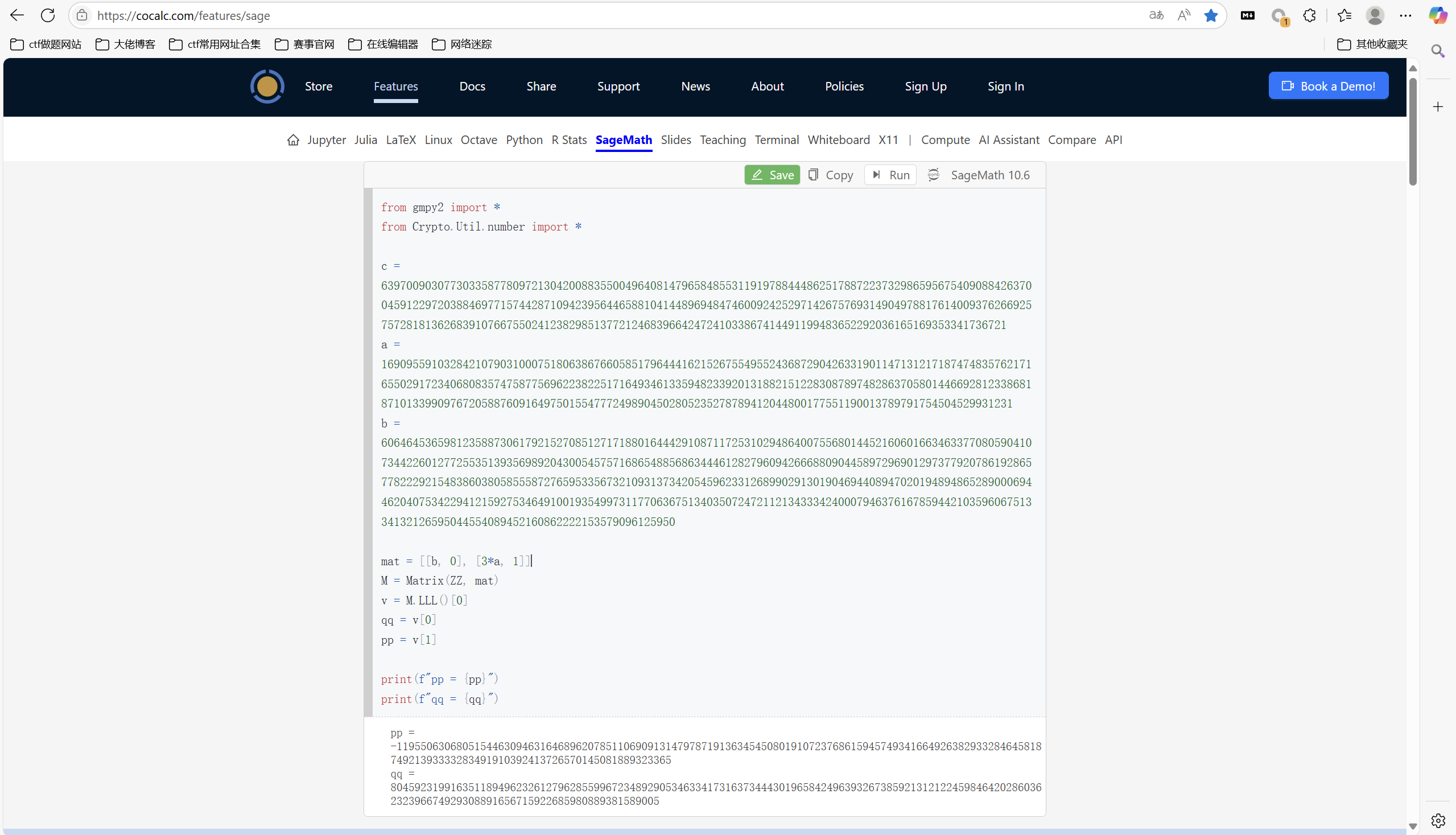

exp：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
import gmpy2
import libnum

pp = 11955063068051544630946316468962078511069091314797871913634545080191072376861594574934166492638293328464581874921393333283491910392413726570145081889323365

qq = 8045923199163511894962326127962855996723489290534633417316373444301965842496393267385921312122459846420286036232396674929308891656715922685980889381589005

c = 63970090307730335877809721304200883550049640814796584855311919788444862517887223732986595675409088426370045912297203884697715744287109423956446588104144896948474600924252971426757693149049788176140093762669257572818136268391076675502412382985137721246839664247241033867414491199483652292036165169353341736721

for i in range(2 ** 8, 2 ** 9):
    for j in range(70):
        p = pp - 2 * i
        q = qq + j
        phi = (p - 1) * (q - 1)
        if gmpy2.gcd(phi, 65537) != 1:
            continue
        d = gmpy2.invert(65537, phi)
        n = p * q
        m = pow(c, d, n)
        flag = libnum.n2s(int(m))
        if b'flag' in flag:
            print(flag)
            break

运行得到flag

1
flag{u_are_@_master_of_latt1ce_Crypt0gr@phy}

没 e 也能玩

题目描述：

1
哎，不是哥们，没 e 居然也能玩

下载附件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
from Crypto.Util.number import *
from gmpy2 import *
from secret import flag

p = getPrime(1024)
q = getPrime(1024)
d = inverse(65537,(p-1)*(q-1))
dp = d %(p-1)
dq = d%(q-1)
print(f'c={pow(bytes_to_long(flag),e,p*q)}')
print(f'p={p}')
print(f'q={q}')
print(f'dp={dp}')
print(f'dq={dq}')

''''
c=312026920216195772014255984174463085443866592575942633449581804171108045852080517840578408476885673600123673447592477875543106559822653280458539889975125069364584140981069913341705738633426978886491359036285144974311751490792757751756044409664421663980721578870582548395096887840688928684149014816557276765747135567714257184475027270111822159712532338590457693333403200971556224662094381891648467959054115723744963414673861964744567056823925630723343002325605154661959863849738333074326769879861280895388423162444746726568892877802824353858845944856881876742211956986853244518521508714633279380808950337611574412909
p=108043725609186781791705090463399988837848128384507136697546885182257613493145758848215714322999196482303958182639388180063206708575175264502030010971971799850889123915580518613554382722069874295016841596099030496486069157061211091761273568631799006187376088457421848367280401857536410610375012371577177832001
q=121590551121540247114817509966135120751936084528211093275386628666641298457070126234836053337681325952068673362753408092990553364818851439157868686131416391201519794244659155411228907897025948436021990520853498462677797392855335364006924106615008646396883330251028071418465977013680888333091554558623089051503
dp=11282958604593959665264348980446305500804623200078838572989469798546944577064705030092746827389207634235443944672230537015008113180165395276742807804632116181385860873677969229460704569172318227491268503039531329141563655811632035522134920788501646372986281785901019732756566066694831838769040155501078857473
dq=46575357360806054039250786123714177813397065260787208532360436486982363496441528434309234218672688812437737096579970959403617066243685956461527617935564293219447837324227893212131933165188205281564552085623483305721400518031651417947568896538797580895484369480168587284879837144688420597737619751280559493857
'''

考点:dp，dq 泄露

一把梭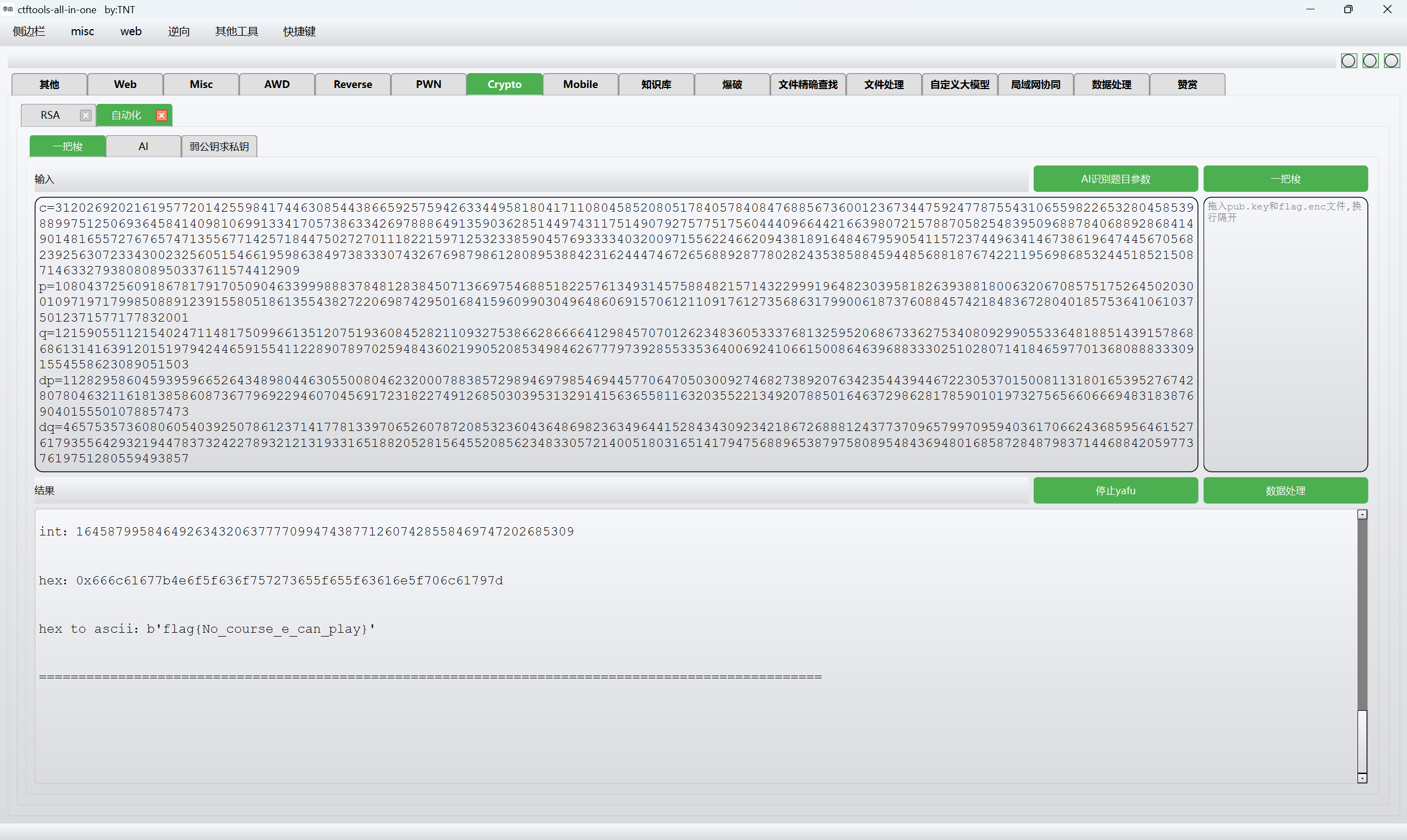

最后flag为

1
flag{No_course_e_can_play}
文章作者: yiqing
文章链接: http://yiqing.asia/posts/192133.html
版权声明: 本博客所有文章除特別声明外，均采用 CC BY 4.0 许可协议。转载请注明来源 yiqing !
newstarctf
赏
  目录